题目内容

设椭圆
x2
4
+
y2
2
=1的两个焦点是F1，F2，点P在椭圆上，且
PF1
•
PF2
=1，那么点P到椭圆中心的距离是（　　）
分析：首先求出F1（
2
，0），F2（-
2
，0），并设p点坐标，根据向量积运算得出x02+y02=3，再由p在椭圆上得出x02+2y02=4，联立两个方程即可求出p点坐标，进而由点到直线的距离的答案．
解答：解：由题意知F1（
2
，0），F2（-
2
，0），设p（x0，y0）
∵
PF1
•
PF2
=1，
∴（
2
-x0，-y0）•（-
2
-x0，-y0）=1即x02+y02=3  ①
又∵x02+2y02=4    ②
联立①②得x0=±
2
  y0=±1
p点到椭圆中心的距离为
3
．
故选B．
点评：本题考查了椭圆的简单性质以及向量的相关运算，问题比较简单，做题时要认真，属于中档题．
练习册系列答案
相关题目
设动直线l垂直x轴，且与椭圆
x2
4
+
y2
2
=1交于A、B两点，P是l上满足|PA|•|PB|=1的点，求P点的轨迹．
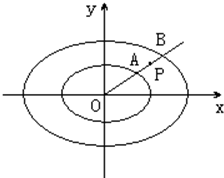精英家教网若椭圆E1：
x2
a
2
1
+
y2
b
2
1
=1和椭圆E2：
x2
a
2
2
+
y2
b
2
2
=1满足
a2
a1
=
b2
b1
=m
 (m＞0)
，则称这两个椭圆相似，m称为其相似比．
（1）求经过点(2，
6
)，且与椭圆
x2
4
+
y2
2
=1相似的椭圆方程；
（2）设过原点的一条射线l分别与（1）中的两个椭圆交于A、B两点（其中点A在线段OB上），
求|OA|+
1
|OB|
的最大值和最小值；
（3）对于真命题“过原点的一条射线分别与相似比为2的两个椭圆C1：
x2
22
+
y2
(
2
)2
=1和C2：
x2
42
+
y2
(2
2
)2
=1交于A、B两点，P为线段AB上的一点，若|OA|、|OP|、|OB|成等差数列，则点P的轨迹方程为
x2
32
+
y2
(
3
2
2
)2
=1”．请用推广或类比的方法提出类似的一个真命题，并给予证明．
（2012•嘉定区三模）如图，在平面直角坐标系xOy中，M、N分别是椭圆
x2
4
+
y2
2
=1的顶点．过坐标原点的直线交椭圆于A、B两点，其中A在第一象限．过点A作x轴的垂线，垂足为C．设直线AB的斜率为k．
（1）若直线AB平分线段MN，求k的值；
（2）当k=2时，求点A到直线BC的距离．
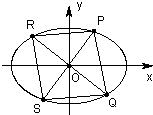精英家教网已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的一个焦点到长轴的两个端点的距离分别为2+
3
和2-
3
．
（1）求椭圆的方程；
（2）若过椭圆的右焦点，倾斜角为
π
3
的直线交椭圆于A、B两点，求线段AB的长；
（3）如图，过原点相互垂直的两条直线与椭圆
x2
4
+
y2
2
=1的四个交点构成四边形PRSQ，设直线PS的倾斜角为θ(θ∈(0，
π
2
])，试问：△PSQ能否为正三角形，若能求θ的值，若不能，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网