题目内容
对于函数 ,若存在区间
,若存在区间 ,使得
,使得 ,则称函数
,则称函数 为“可等域函数”,区间
为“可等域函数”,区间 为函数
为函数 的一个“可等域区间”.给出下列4个函数:
的一个“可等域区间”.给出下列4个函数:
① ;②
;② ; ③
; ③ ; ④
; ④ .
.
其中存在唯一“可等域区间”的“可等域函数”为( )
| A.①②③ | B.②③ | C.①③ | D.②③④ |
B
解析试题分析:根据题意,①中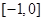 与
与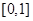 都是
都是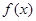 的可等域区间,②中,
的可等域区间,②中,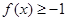 ,且
,且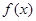 在
在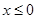 时递减,在
时递减,在 时递增,若
时递增,若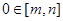 ,则
,则 ,于是
,于是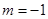 ,又
,又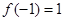 ,
,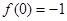 ,而
,而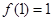 ,故
,故 ,
,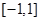 是一个可等域区间,有没有可等域区间
是一个可等域区间,有没有可等域区间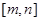 ,且
,且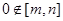 呢?若
呢?若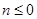 ,则
,则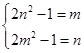 ,解得
,解得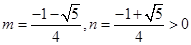 ,不合题意,若
,不合题意,若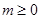 ,则
,则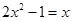 有两个非负解,但此方程的两解为1和
有两个非负解,但此方程的两解为1和 ,也不合题意,故函数
,也不合题意,故函数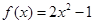 只有一个等可域区间
只有一个等可域区间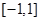 ,③中函数
,③中函数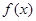 的值域是
的值域是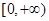 ,所以
,所以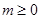 ,函数
,函数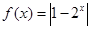 在
在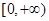 上是增函数,考察方程
上是增函数,考察方程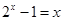 ,由于函数
,由于函数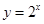 与
与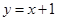 只有两个交点
只有两个交点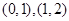 ,即方程
,即方程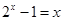 只有两个解0和1,因此此函数只有一个等可域区间
只有两个解0和1,因此此函数只有一个等可域区间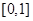 ,对于④,函数
,对于④,函数 在定义域
在定义域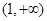 上是增函数,若上函数有等可域区间
上是增函数,若上函数有等可域区间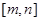 ,则
,则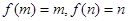 ,但方程
,但方程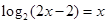 无解(方程
无解(方程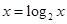 无解),故此函数无可等域区间.综上只有②③正确,选B.
无解),故此函数无可等域区间.综上只有②③正确,选B.
考点:函数的定义域与值域,单调性,方程的解等综合问题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
若函数 在区间
在区间 上存在一个零点,则实数
上存在一个零点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. 或 或 | D. |
函数 为定义在R上的偶函数,且当
为定义在R上的偶函数,且当 时,
时, 则下列选项正确的是( )
则下列选项正确的是( )
A. | B. | C. | D. |
已知函数 是定义在
是定义在 上的偶函数,且
上的偶函数,且 ,则下列各式中一定成立
,则下列各式中一定成立
的是( ).
A. | B. |
C. | D.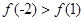 |
已知 ,
, ,规定:当
,规定:当 时,
时,  ;当
;当 时,
时,  ,则
,则 ( )
( )
A.有最小值 ,最大值1 ,最大值1 | B.有最大值1,无最小值 |
C.有最小值 ,无最大值 ,无最大值 | D.有最大值 ,无最小值 ,无最小值 |
已知函数f(x)满足f(x)=f(π-x),且当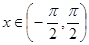 时,f(x)=x+sinx,则( )
时,f(x)=x+sinx,则( )
| A.f(1)<f(2)<f(3) | B.f(2)<f(3)<f(1) |
| C.f(3)<f(2)<f(1) | D.f(3)<f(1)<f(2) |
下列函数中,与函数 的奇偶性、单调性均相同的是( )
的奇偶性、单调性均相同的是( )
A. | B. | C. | D. |
 图象中,满足
图象中,满足 的只可能是( )
的只可能是( )
 :函数
:函数 的图象恒过定点
的图象恒过定点 ;命题
;命题 :若函数
:若函数
 为偶函数,则函数
为偶函数,则函数 的图象关于直线
的图象关于直线 对称,则下列命题为真命题的是( )
对称,则下列命题为真命题的是( )


