题目内容
函数f（x）在（-∞，+∞）上是奇函数，当x∈（-∞，0]时，f（x）=2x（x-1），则f（x）= ．
【答案】分析：要求函数f（x）的解析式，仅求出x＜0的解析式即可，根据x＜0与x＞0之间的关系将未知区间转化到已知区间上，再利用函数的奇偶性求出x＜0的解析式．
解答：解：当x＞0时，-x＜0
因为x∈（-∞，0]时f（x）=2x（x-1），
所以f（-x）=-2x（-x-1），
因为f（x）是奇函数，所以f（-x）=-f（x），
所以x＞0时，f（x）=-f（-x）=2x（-x-1）=-2x（x+1）．
所以f（x）的解析式为f（x）=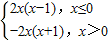
故答案为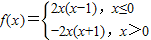
点评：本题主要考察函数奇偶性在求解析式中的应用，属中档题．
解答：解：当x＞0时，-x＜0
因为x∈（-∞，0]时f（x）=2x（x-1），
所以f（-x）=-2x（-x-1），
因为f（x）是奇函数，所以f（-x）=-f（x），
所以x＞0时，f（x）=-f（-x）=2x（-x-1）=-2x（x+1）．
所以f（x）的解析式为f（x）=
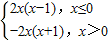
故答案为
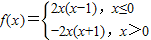
点评：本题主要考察函数奇偶性在求解析式中的应用，属中档题．
练习册系列答案
相关题目
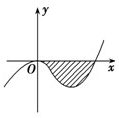已知函数f（x）=x3+ax2+bx+c的图象如图，直线y=0在原点处与函数图象相切，且此切线与函数图象所围成的区域（阴影）面积为
（2014•达州一模）已知二次函数h（x）=ax2+bx+c（其中c＜3），其导函数y=h′（x）的图象如图，f（x）=6lnx+h（x）．