题目内容
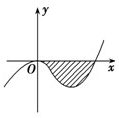已知函数f（x）=x3+ax2+bx+c的图象如图，直线y=0在原点处与函数图象相切，且此切线与函数图象所围成的区域（阴影）面积为| 27 | 4 |
（1）求f（x）的解析式
（2）若常数m＞0，求函数f（x）在区间[-m，m]上的最大值．
分析：（1）根据图象所过点（0，0），及y=0与在原点处与函数图象相切可求b，c，由题目中给出了区域的面积，我们可以从定积分着手，求出函数以及函数与x轴的交点，建立方程可求解参数．
（2）利用导数求出函数的极值，求出函数的零点，分0＜m≤3，m＞3两种情况进行讨论，借助图象可求得函数的最大值；
（2）利用导数求出函数的极值，求出函数的零点，分0＜m≤3，m＞3两种情况进行讨论，借助图象可求得函数的最大值；
解答：解：（1）由图象知，f（0）=0，得c=0，
f′（x）=3x2+2ax+b，由f′（0）=0，得b=0，
∴f（x）=x3+ax2=x2（x+a），
令f（x）=0，可得x=0或者x=-a，
可以得到图象与x轴交点为（0，0），（-a，0），
故对-f（x）从0到-a求定积分即为所求面积，即
[-f（x）]dx=
，
∫0-a（-x3-ax2）dx=
，解得a=-3．
∴f（x）=x3-3x2；
（2）由（1）知f'（x）=3x2-6x=3x（x-2）．则x，f'（x），f（x）的取值变化情况如下表：
又f（3）=0，
①当0＜m≤3时，f（x）max=f（0）=0；
②当m＞3时，f(x)max=f(m)=m3-3m2．
综上可知f(x)max=
．
f′（x）=3x2+2ax+b，由f′（0）=0，得b=0，
∴f（x）=x3+ax2=x2（x+a），
令f（x）=0，可得x=0或者x=-a，
可以得到图象与x轴交点为（0，0），（-a，0），
故对-f（x）从0到-a求定积分即为所求面积，即
| ∫ | -a 0 |
| 27 |
| 4 |
∫0-a（-x3-ax2）dx=
| 27 |
| 4 |
∴f（x）=x3-3x2；
（2）由（1）知f'（x）=3x2-6x=3x（x-2）．则x，f'（x），f（x）的取值变化情况如下表：
| x | （-∞，0） | 0 | （0，2） | 2 | （2，+∞） |
| f'（x） | + | 0 | - | 0 | + |
| f（x） | 单调递增 | 极大值f（0）=0 | 单调递减 | 极小值f（2）=-4 | 单调递增 |
①当0＜m≤3时，f（x）max=f（0）=0；
②当m＞3时，f(x)max=f(m)=m3-3m2．
综上可知f(x)max=
|
点评：将函数图象、函数的导数以及定积分的计算有机结合起来综合考查，考查了学生的综合能力．
练习册系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|