题目内容
8、点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为( )
分析:欲求PA与BD所成角的度数,必须先找出异面直线CD1和BC1所成的角,将图形补成一个正方体如图,利用正方体中线间的平行关系,即可知道是哪一个角即为所求,最后解三角形即得.
解答: 解析:将图形补成一个正方体如图,则PA与BD所成角等于BC′与BD所成角即∠DBC′.
解析:将图形补成一个正方体如图,则PA与BD所成角等于BC′与BD所成角即∠DBC′.
在等边三角形DBC′中,∠DBC′=60°,即PA与BD所成角为60°.
故选C.
 解析:将图形补成一个正方体如图,则PA与BD所成角等于BC′与BD所成角即∠DBC′.
解析:将图形补成一个正方体如图,则PA与BD所成角等于BC′与BD所成角即∠DBC′.在等边三角形DBC′中,∠DBC′=60°,即PA与BD所成角为60°.
故选C.
点评:本题主要考查了异面直线及其所成的角、补形法,以及空间想象力、特殊化思想方法,属于基础题.

练习册系列答案
相关题目
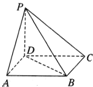 如图,点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为( )
如图,点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为( )| A、30° | B、45° | C、60° | D、90° |
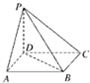 如图所示,点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为
如图所示,点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为 如图,在棱长为1的正方体AC1中,E、F分别为A1D1和A1B1的中点.
如图,在棱长为1的正方体AC1中,E、F分别为A1D1和A1B1的中点. 如图:点P在正方形ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个命题:
如图:点P在正方形ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个命题: 如图,在棱长为1的正方体AC1中,E、F分别为A1D1和A1B1的中点.
如图,在棱长为1的正方体AC1中,E、F分别为A1D1和A1B1的中点.