题目内容
 如图:点P在正方形ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个命题:
如图:点P在正方形ABCD-A1B1C1D1的面对角线BC1上运动,则下列四个命题:①C1B与平面ABCD所成的角为45°;
②三棱锥A-D1PC的体积不变;
③A1P∥面ACD1;
④DP⊥BC1.
其中正确的命题的序号是
①②③
①②③
.分析:对于①,CB为C1B在平面ABCD中的射影,所以∠C1BC为C1B与平面ABCD所成的角,等于45°;
对于②,可以证明BC1∥平面AD1C,故BC1上任意一点到平面AD1C的距离均相等,所以三棱锥A-D1PC的体积不变;
对于③,可证面BA1C1∥面ACD1,从而由面面平行的性质可得A1P∥面ACD1;
对于④,由于DC⊥平面BCB1C1,所以DC⊥BC1,若DP⊥BC1,则DC与DP重合,与条件矛盾.
对于②,可以证明BC1∥平面AD1C,故BC1上任意一点到平面AD1C的距离均相等,所以三棱锥A-D1PC的体积不变;
对于③,可证面BA1C1∥面ACD1,从而由面面平行的性质可得A1P∥面ACD1;
对于④,由于DC⊥平面BCB1C1,所以DC⊥BC1,若DP⊥BC1,则DC与DP重合,与条件矛盾.
解答: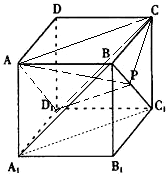 解:对于①,CB为C1B在平面ABCD中的射影,所以∠C1BC为C1B与平面ABCD所成的角,等于45°,故正确;
解:对于①,CB为C1B在平面ABCD中的射影,所以∠C1BC为C1B与平面ABCD所成的角,等于45°,故正确;
对于②,∵AD1∥BC1,BC1?平面AD1C,AD1?平面AD1C,∴BC1∥平面AD1C,故BC1上任意一点到平面AD1C的距离均相等,所以以P为顶点,平面AD1C为底面,三棱锥A-D1PC的体积不变,故正确;
对于③,连接A1B,A1C1,则A1C1∥AC,∵AD1∥BC1∴面BA1C1∥面ACD1,从而由面面平行的性质可得A1P∥面ACD1,故正确;
对于④,由于DC⊥平面BCB1C1,所以DC⊥BC1,若DP⊥BC1,则DC与DP重合,与条件矛盾,故不正确;
综上知,①②③
故答案为:①②③
 解:对于①,CB为C1B在平面ABCD中的射影,所以∠C1BC为C1B与平面ABCD所成的角,等于45°,故正确;
解:对于①,CB为C1B在平面ABCD中的射影,所以∠C1BC为C1B与平面ABCD所成的角,等于45°,故正确;对于②,∵AD1∥BC1,BC1?平面AD1C,AD1?平面AD1C,∴BC1∥平面AD1C,故BC1上任意一点到平面AD1C的距离均相等,所以以P为顶点,平面AD1C为底面,三棱锥A-D1PC的体积不变,故正确;
对于③,连接A1B,A1C1,则A1C1∥AC,∵AD1∥BC1∴面BA1C1∥面ACD1,从而由面面平行的性质可得A1P∥面ACD1,故正确;
对于④,由于DC⊥平面BCB1C1,所以DC⊥BC1,若DP⊥BC1,则DC与DP重合,与条件矛盾,故不正确;
综上知,①②③
故答案为:①②③
点评:本题考查三棱锥体积求法中的等体积法,考查线面平行、垂直的判定,考查线面角,综合性强.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
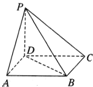 如图,点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为( )
如图,点P在正方形ABCD所在平面外,PD⊥平面ABCD,PD=AD,则PA与BD所成角的度数为( )| A、30° | B、45° | C、60° | D、90° |