题目内容
 如图,从圆O外一点P引圆O的割线PAB和PCD,PCD过圆心O,已知PA=1,AB=2,PO=3,则圆O的半径等于
如图,从圆O外一点P引圆O的割线PAB和PCD,PCD过圆心O,已知PA=1,AB=2,PO=3,则圆O的半径等于| 6 |
| 6 |
分析:由于PAB与PCD是圆的两条割线,且PA=1,AB=2,PO=3,我们可以设圆的半径为R,然后根据切割线定理构造一个关于R的方程,解方程即可求解.
解答:解:设⊙O的半径为R
则PC=PO-OC=3-R
PD=PO+OD=3+R
又∵PA=1,AB=2,
∴PB=PA+AB=3
由切割线定理易得:
PA•PB=PC•PD
即1×3=(3-R)×(3+R)
解得R=
.
故答案:
.
则PC=PO-OC=3-R
PD=PO+OD=3+R
又∵PA=1,AB=2,
∴PB=PA+AB=3
由切割线定理易得:
PA•PB=PC•PD
即1×3=(3-R)×(3+R)
解得R=
| 6 |
故答案:
| 6 |
点评:本题考查的知识点是与圆相关的比例线段,设出未知的线段根据圆幂定理列出满足条件的方程是解答的关键.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
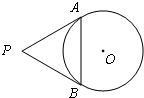 如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么点P与O间的距离是( )
如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么点P与O间的距离是( )| A、16 | ||||
| B、20 | ||||
C、
| ||||
D、
|
 如图,从圆O外一点P引圆O的切线PA和割线PBC,已知
如图,从圆O外一点P引圆O的切线PA和割线PBC,已知 如图,从圆O外一点P引两条直线分别交圆O于点A,B,C,D,且PA=AB,PC=5,CD=9,则AB的长等于
如图,从圆O外一点P引两条直线分别交圆O于点A,B,C,D,且PA=AB,PC=5,CD=9,则AB的长等于 附加题 选做题在A、B、C、D四小题中只能选做两小题,每小题10分,共计20分,解答时应写出文字说明、证明过程或演算步骤.
附加题 选做题在A、B、C、D四小题中只能选做两小题,每小题10分,共计20分,解答时应写出文字说明、证明过程或演算步骤. (2013•房山区一模)如图,从圆O外一点P引圆O的切线PA和割线PBC,已知∠BPA=30°,BC=11,PB=1,则PA=
(2013•房山区一模)如图,从圆O外一点P引圆O的切线PA和割线PBC,已知∠BPA=30°,BC=11,PB=1,则PA=