题目内容
(1)(选修4-2 矩阵与变换)已知矩阵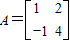 ,向量
,向量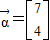 .
.①求矩阵A的特征值λ1、λ2和特征向量
 、
、 ;
;②求A5
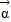 的值.
的值.(2)选修4-4:坐标系与参数方程求极坐标系中,圆ρ=2上的点到直线
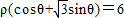 的距离的最小值.
的距离的最小值.(3)选修4-5;不等式选讲知x,y,z为正实数,且
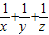 =1,求x+4y+9z的最小值及取得最小值时x,y,z的值.
=1,求x+4y+9z的最小值及取得最小值时x,y,z的值.
【答案】分析:(1)①先求出矩阵A的特征多项式,令特征多项式等于零,求得特征值,即可求得特征向量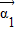 、
、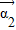 .
.
②由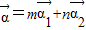 求得m、n的值,再由
求得m、n的值,再由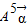 =
=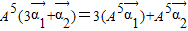 ,运算求得结果.
,运算求得结果.
(2)把圆、直线的极坐标方程化为直角坐标方程,求出圆心到直线的距离,再将此距离减去半径,即得所求.
(3)由柯西不等式得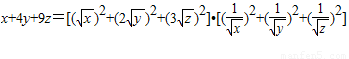 ,再利用基本
,再利用基本
不等式求得它的最小值.
解答:解:(1)①矩阵A的特征多项式为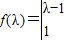
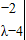 =λ2-5λ+6,令f(λ)=0,得λ1=2,λ2=3,
=λ2-5λ+6,令f(λ)=0,得λ1=2,λ2=3,
当λ1=2时,得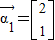 ,当λ2=3时,得
,当λ2=3时,得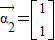 .…(3分)
.…(3分)
②由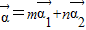 得
得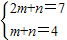 ,得m=3,n=1.
,得m=3,n=1.
∴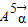 =
=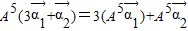 =
=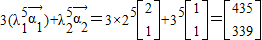 .…(7分)
.…(7分)
(2)解:由 ρ=2即ρ2=4,则易得x2+y2=4,由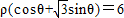 易得
易得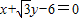 ,
,
∴圆心(0,0)到直线的距离为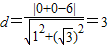 ,
,
∵又圆的半径为2,
∴圆上的点到直线的距离的最小值为d=d-2=3-2=1.…(7分)
(3)解:由柯西不等式得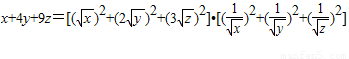
≥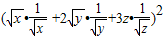 =36,
=36,
当且仅当x=2y=3z时等号成立,此时x=6,y=3,z=2,
所以当x=6,y=3,z=2时,x+4y+9z取得最小值36.…(7分)
点评:本题主要考查点的极坐标与直角坐标的互化,矩阵的特征值与特征向量,柯西不等式的应用,属于基础题.
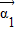 、
、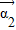 .
.②由
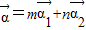 求得m、n的值,再由
求得m、n的值,再由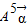 =
=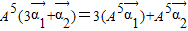 ,运算求得结果.
,运算求得结果.(2)把圆、直线的极坐标方程化为直角坐标方程,求出圆心到直线的距离,再将此距离减去半径,即得所求.
(3)由柯西不等式得
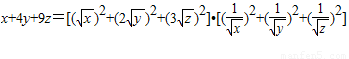 ,再利用基本
,再利用基本不等式求得它的最小值.
解答:解:(1)①矩阵A的特征多项式为
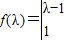
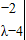 =λ2-5λ+6,令f(λ)=0,得λ1=2,λ2=3,
=λ2-5λ+6,令f(λ)=0,得λ1=2,λ2=3,当λ1=2时,得
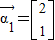 ,当λ2=3时,得
,当λ2=3时,得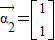 .…(3分)
.…(3分)②由
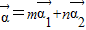 得
得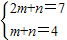 ,得m=3,n=1.
,得m=3,n=1.∴
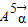 =
=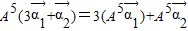 =
=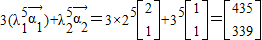 .…(7分)
.…(7分)(2)解:由 ρ=2即ρ2=4,则易得x2+y2=4,由
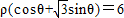 易得
易得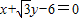 ,
,∴圆心(0,0)到直线的距离为
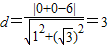 ,
,∵又圆的半径为2,
∴圆上的点到直线的距离的最小值为d=d-2=3-2=1.…(7分)
(3)解:由柯西不等式得
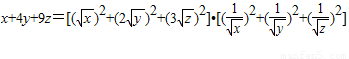
≥
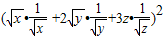 =36,
=36,当且仅当x=2y=3z时等号成立,此时x=6,y=3,z=2,
所以当x=6,y=3,z=2时,x+4y+9z取得最小值36.…(7分)
点评:本题主要考查点的极坐标与直角坐标的互化,矩阵的特征值与特征向量,柯西不等式的应用,属于基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 是将平面上每个点
是将平面上每个点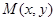 的横坐标乘2,纵坐标乘4,变到点
的横坐标乘2,纵坐标乘4,变到点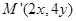 。
。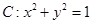 在变换
在变换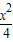 +
+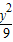 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.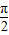 ),若直线l过点P,且倾斜角为
),若直线l过点P,且倾斜角为 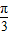 ,圆C以M为圆心、4为半径.
,圆C以M为圆心、4为半径.