题目内容
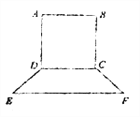
【题目】要制作一个如图的框架（单位：米）.要求所围成的总面积为19.5（
），其中
是一个矩形， 
是一个等腰梯形，梯形高
， 
，设
米， 
米.
（1）求
关于
的表达式；
（2）如何设计，的长度，才能使所用材料最少？
【答案】（1）y＝
－
x
（2）AB＝3m，BC＝4m
【解析】
(1)如图，在等腰梯形CDEF中，DH是高．
依题意：DH＝
AB＝x，EH＝
×x＝
x，
∴
＝xy＋ 
x＝xy＋
x2，∴y＝
－x.
∵x＞0，y＞0，∴－x＞0，解之得0＜x＜
.
∴所求表达式为y＝－x
.
(2)在Rt△DEH中，∵tan∠FED＝
，∴sin∠FED＝
，
∴DE＝
＝x×
＝x，
∴l＝(2x＋2y)＋2×x＋
＝2y＋6x＝
－x＋6x＝＋
x≥2
＝26，
当且仅当＝x，即x＝3时取等号，
此时y＝－x＝4，
∴AB＝3m，BC＝4m时，能使整个框架所用材料最少．
【题目】为了解春季昼夜温差大小与某种子发芽数之间的关系，现在从4月份的30天中随机挑选了5天进行研究，且分别记录了明天昼夜温差与每天100颗种子浸泡后的发芽数，得到如下表格：
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
从这5天中任选2天，记发芽的种子数分别为
，求事件“君不小于25”的概率；
（2）从这5天中任选2天，若选取的是4月1日与4月30日的两组数据，请根据这5填中的另三天的数据，求出
关于
的线性回归方程，
.
（参考公式：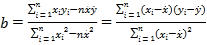
，
）.
【题目】电动摩托车的续航里程，是指电动摩托车在蓄电池满电量的情况下一次能行驶的最大距离.为了解A，B两个不同型号电动摩托车的续航里程，现从某卖场库存电动摩托车中随机抽取A，B两个型号的电动摩托车各5台，在相同条件下进行测试，统计结果如下：
电动摩托车编号 | 1 | 2 | 3 | 4 | 5 |
A型续航里程（km） | 120 | 125 | 122 | 124 | 124 |
B型续航里程（km） | 118 | 123 | 127 | 120 | a |
已知A，B两个型号被测试电动摩托车续航里程的平均值相等.
（1）求a的值；
（2）求A型号被测试电动摩托车续航里程标准差的大小；
（3）从被测试的电动摩托车中随机抽取A，B型号电动摩托车各1台，求至少有1台的续航里程超过122km的概率.
（注：n个数据
，的方差
，其中
为数据的平均数）
