题目内容
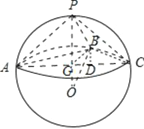
【题目】已知P,A,B,C是半径为2的球面上的点,PA=PB=PC=2,![]() ,点B在AC上的射影为D,则三棱锥
,点B在AC上的射影为D,则三棱锥![]() 体积的最大值为( )
体积的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
先画出图形(见解析),求出三棱锥的高,由题意得出三棱锥![]() 体积最大时
体积最大时![]() 面积最大,进而求出
面积最大,进而求出![]() 的面积表达式,利用函数知识求出面积最大值,从而求出三棱锥
的面积表达式,利用函数知识求出面积最大值,从而求出三棱锥![]() 体积最大值.
体积最大值.
如下图,由题意,![]() ,
,![]() ,
,
取![]() 的中点为
的中点为![]() ,则
,则![]() 为三角形
为三角形![]() 的外心,且为
的外心,且为![]() 在平面
在平面![]() 上的射影,所以球心在
上的射影,所以球心在![]() 的延长线上,设
的延长线上,设![]() ,则
,则![]() ,
,
所以![]() ,即
,即![]() ,所以
,所以![]() .
.
故![]() ,
,
过![]() 作
作![]() 于
于![]() ,设
,设![]() (
(![]() ),则
),则![]() ,
,
设![]() ,则
,则![]() ,故
,故![]() ,
,
所以![]() ,则
,则![]() ,
,
所以![]() 的面积
的面积![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() ,所以当
,所以当![]() 时,
时,![]() ,即
,即![]() 此时单调递增;当
此时单调递增;当![]() 时,
时,![]() ,此时
,此时![]() 单调递减.
单调递减.
所以当![]() 时,
时,![]() 取到最大值为
取到最大值为![]() ,即
,即![]() 的面积最大值为
的面积最大值为![]() .
.
当![]() 的面积最大时,三棱锥
的面积最大时,三棱锥![]() 体积取得最大值为
体积取得最大值为![]() .
.
故选D.

练习册系列答案
相关题目