题目内容
如图,在平面直角坐标系 中,过
中,过 轴正方向上一点
轴正方向上一点 任作一直线,与抛物线
任作一直线,与抛物线 相交于
相交于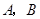 两点.一条垂直于
两点.一条垂直于 轴的直线,分别与线段
轴的直线,分别与线段 和直线
和直线 交于点
交于点 .
.
(1)若 ,求
,求 的值;
的值;
(2)若 为线段
为线段 的中点,求证:
的中点,求证: 为此抛物线的切线;
为此抛物线的切线;
(3)试问(2)的逆命题是否成立?说明理由.

【答案】
解:(1)设直线 的方程为
的方程为 ,
,
将该方程代入 得
得 .
.
令 ,
, ,则
,则 .
.
因为 ,解得
,解得 ,
,
或 (舍去).故
(舍去).故 .
.
(2)由题意知 ,直线
,直线 的斜率为
的斜率为 .
.
又 的导数为
的导数为 ,所以点
,所以点 处切线的斜率为
处切线的斜率为 ,
,
因此, 为该抛物线的切线.
为该抛物线的切线.
(3)(2)的逆命题成立,证明如下:
设 .
.
若 为该抛物线的切线,则
为该抛物线的切线,则 ,
,
又直线 的斜率为
的斜率为 ,所以
,所以 ,
,
得 ,因
,因 ,有
,有 .
.
故点 的横坐标为
的横坐标为 ,即
,即 点是线段
点是线段 的中点.
的中点.
【解析】略

练习册系列答案
相关题目
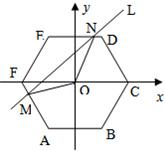 如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )
如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )| A、偶函数 | B、奇函数 | C、不是奇函数,也不是偶函数 | D、奇偶性与k有关 |
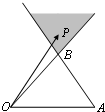 如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且
如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且 1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
 (2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是
(2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是