题目内容
已知向量 且
且 ,
,(Ⅰ)若
 与
与 是两个共线向量,求x的值;
是两个共线向量,求x的值;(Ⅱ)若
 ,求函数f(x)的最小值及相应的x的值.
,求函数f(x)的最小值及相应的x的值.
【答案】分析:(Ⅰ)利用向量共线的充要条件列出三角方程,求出cos2x的值,根据角的范围求出角x.
(Ⅱ)利用向量的数量积求出函数f(x),利用二倍角公式化简f(x),利用基本不等式求出函数的最小值.
解答:解:(Ⅰ)∵ ∥
∥
∴ ,
,
又∵
∴sinx≠0,2x∈(0,π]
∴ 即
即
∴ .
.
(Ⅱ)
当且仅当 即
即 时取到等号.
时取到等号.
故函数f(x)的最小值为 ,此时
,此时 .
.
点评:本题考查向量共线的充要条件、解三角方程、向量的数量积公式、利用基本不等式求最值.
(Ⅱ)利用向量的数量积求出函数f(x),利用二倍角公式化简f(x),利用基本不等式求出函数的最小值.
解答:解:(Ⅰ)∵
 ∥
∥
∴
 ,
,又∵

∴sinx≠0,2x∈(0,π]
∴
 即
即
∴
 .
.(Ⅱ)

当且仅当
 即
即 时取到等号.
时取到等号.故函数f(x)的最小值为
 ,此时
,此时 .
.点评:本题考查向量共线的充要条件、解三角方程、向量的数量积公式、利用基本不等式求最值.

练习册系列答案
相关题目
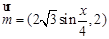 ,
,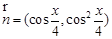 .函数
.函数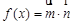 .
.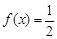 ,求
,求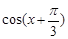 的值;
的值;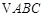 中,角
中,角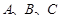 的对边分别是
的对边分别是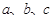 ,且满足
,且满足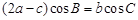 ,
,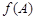 的取值范围.
的取值范围.