题目内容
设点A(2,-3),B(-3,-2),直线l过点P(1,1)且与线段AB相交,则直线l的斜率k的取值范围是( )。
A.k≥ 或k≤-4 或k≤-4 | B.k≥ 或k≤- 或k≤- |
C.-4≤k≤ | D. ≤k≤4 ≤k≤4 |
A
解析试题分析:画出图形,由题意得所求直线l的斜率k满足
 ,用直线的斜率公式求出
,用直线的斜率公式求出 和
和 的值,求出直线l的斜率k的取值范围. 解:如图所示:由题意得,所求直线l的斜率k满足
的值,求出直线l的斜率k的取值范围. 解:如图所示:由题意得,所求直线l的斜率k满足
 ,即
,即 
即直线的斜率的取值范围是k≥ 或k≤-4 ,故选A
或k≤-4 ,故选A
考点:直线的斜率
点评:本题考查直线的斜率公式的应用,体现了数形结合的数学思想,解题的关键是利用了数形结合的思想,解题过程较为直观,本题类似的题目比较多.可以移动一个点的坐标,变式出其他的题目.

练习册系列答案
相关题目
已知直线l1: y=x·sinα和直线l2: y="2x+c," 则直线l1与l2 ( )
| A.通过平移可以重合 | B.不可能垂直 |
| C.可能与x轴围成等腰直角三角形 | D.通过绕l1上某点旋转可以重合 |
如果直线(3a+2)x+ay-1=0与直线2ax+y-2a+1=0互相平行,则实数a的值为 ( )
A.0或- | B.- | C.2 | D.2或- |
已知直线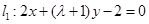 ,
, ,若
,若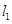 ∥
∥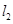 ,则
,则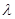 的值是( )
的值是( )
A.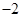 | B. | C.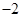 或1 或1 | D.1 |
直线 的倾斜角的正切值为-
的倾斜角的正切值为- ,直线
,直线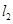 与
与 垂直,则
垂直,则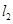 的斜率是( )
的斜率是( )
A. | B. | C.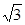 | D. |
已知点 、
、 直线
直线 过点
过点 ,且与线段AB相交,则直线
,且与线段AB相交,则直线 的斜率的取值
的斜率的取值 范围是 ( )
范围是 ( )
A. 或 或 | B. 或 或 | C. | D. |
已知直线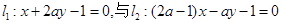 平行,则
平行,则 的值是( )
的值是( )
| A.0或1 | B.1或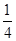 | C.0或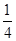 | D.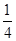 |
过点(1,2)且与原点的距离最大的直线方程是( )
| A.2x+y-4=0 | B.x+2y-5="0" | C.x+3y-7=0 | D.3x+y-5=0 |
 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为( )



