题目内容
(本小题满分12分)
已知数列{an}中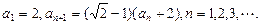
(Ⅰ)求{an}的通项公式;
(Ⅱ)若数列{bn}中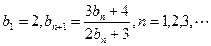 ,证明:
,证明:
 ≤
≤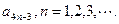
已知数列{an}中
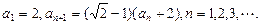
(Ⅰ)求{an}的通项公式;
(Ⅱ)若数列{bn}中
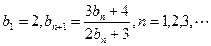 ,证明:
,证明: ≤
≤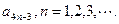
(Ⅰ) 的通项公式为
的通项公式为 ,
,
(Ⅱ)
 的通项公式为
的通项公式为 ,
,
(Ⅱ)

解:(Ⅰ)由题设:


 ,
,
 .
.
所以,数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
 ,
,
即 的通项公式为
的通项公式为 ,
, .
.
(Ⅱ)用数学归纳法证明.
(ⅰ)当 时,因
时,因 ,
, ,所以
,所以
 ,结论成立.
,结论成立.
(ⅱ)假设当 时,结论成立,即
时,结论成立,即 ,
,
也即 .
.
当n=k+1时,

又 ,
,
所以

也就是说,当n=k+1时,结论成立.
根据(i)和(ii)知


 ,
, .
.所以,数列
 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列, ,
,即
 的通项公式为
的通项公式为 ,
, .
.(Ⅱ)用数学归纳法证明.
(ⅰ)当
 时,因
时,因 ,
, ,所以
,所以 ,结论成立.
,结论成立.(ⅱ)假设当
 时,结论成立,即
时,结论成立,即 ,
,也即
 .
.当n=k+1时,

又
 ,
,所以


也就是说,当n=k+1时,结论成立.
根据(i)和(ii)知


练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
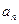 }、{
}、{ 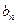 }满足:
}满足: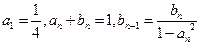 .
.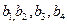 ; (2) 猜想
; (2) 猜想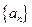 的通项公式,并用数学归纳法证明;
的通项公式,并用数学归纳法证明;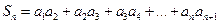 ,求实数
,求实数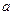 为何值时
为何值时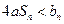 恒成立
恒成立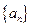 的前
的前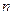 项和为
项和为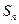 ,且
,且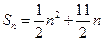 .
.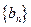 满足
满足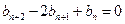 (
(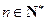 ),且
),且 ,
,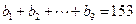 .
.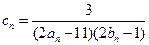 ,数列
,数列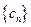 的前
的前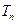 ,求使不等式
,求使不等式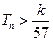 对一切
对一切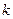 的值;
的值;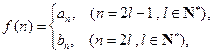 是否存在
是否存在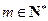 ,使得
,使得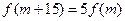 成立?若存在,求出
成立?若存在,求出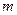 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.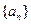 中,
中,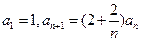
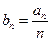 ,证明数列
,证明数列 是等比数列并求数列
是等比数列并求数列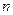 项和
项和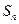
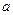 万元,年利率为
万元,年利率为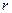 ,按复利计算,从2010年末开始,每年末偿还一定金额,计划第5年底还清,则每年应偿还的金额数为( )万元.
,按复利计算,从2010年末开始,每年末偿还一定金额,计划第5年底还清,则每年应偿还的金额数为( )万元.
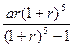
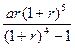
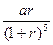
 的前n项和
的前n项和 满足
满足 ,求通项公式
,求通项公式 。
。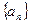 的前
的前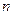 项和为
项和为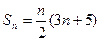 ,正项等比数列
,正项等比数列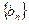 中,
中,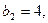
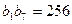 .
.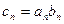 ,求
,求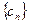 的前
的前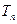 .
.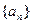 满足对于任意
满足对于任意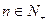 都有
都有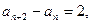 且
且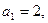 则
则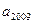 =( )
=( )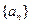 的通项公式为
的通项公式为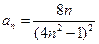 ,
,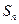 为其前
为其前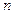 项的和.计算
项的和.计算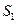 ,
,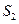 ,
,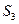 的值,根据计算结果,推测出计算
的值,根据计算结果,推测出计算