Question

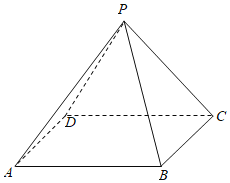
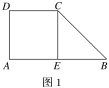
【题目】已知如图1直角梯形，，，，，E为的中点，沿将梯形折起（如图2），使平面平面.

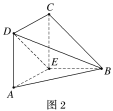
（1）证明：平面；

（2）在线段上是否存在点F，使得平面与平面所成的锐二面角的余弦值为，若存在，求出点F的位置；若不存在，请说明理由.

Answer 1

【答案】（1）见解析；（2）存在，F为中点

【解析】

（1）连接，则，由平面平面可得平面，可得,又可证平面；

（2）建立空间直角坐标系，设，，根据二面角的向量计算公式即可求出.

（1）证明 连接，则，

又平面平面，平面平面，平面，

所以平面，

所以.

又，，，平面，

所以平面.

（2）（1）得平面，所以.

所以，，两两垂直，

分别以，，方向为x，y，z轴正方向，建立空间直角坐标系,

如图所示，

则，，，

设，，

所以，，

设平面的法向量为，

则

取，得.

取平面的法向量为.

所以，

所以.

所以线段上存在点F，且F为中点时，使得平面与平面所成的锐二面角的余弦值为.