题目内容
(本题满分13分)已知点F(1,0),圆E: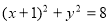 ,点P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.
,点P是圆E上任意一点,线段PF的垂直平分线和半径PE相交于Q.
(1)求动点Q的轨迹Γ的方程;
(2)若直线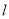 与圆O:
与圆O: 相切,并与(1)中轨迹Γ交于不同的两点A、B.当
相切,并与(1)中轨迹Γ交于不同的两点A、B.当 =
= ,且满足
,且满足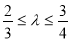 时,求△AOB面积S的取值范围.
时,求△AOB面积S的取值范围.
(1)  ;(2) [
;(2) [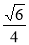 ,
,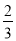 ].
].
【解析】
试题分析:(1)连接QF,∵|QE|+|QF|=|QE|+|QP|=|PE|=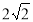 符合椭圆的定义,于是可根据其焦距与长轴计算出短轴长,从而确定
符合椭圆的定义,于是可根据其焦距与长轴计算出短轴长,从而确定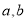 的值,写出动点Q的轨迹Γ的方程;
的值,写出动点Q的轨迹Γ的方程;
(2) 设直线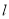 的方程为
的方程为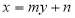 (
( ),由直线与圆相切确定
),由直线与圆相切确定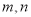 的关系,设点A、B的坐标(
的关系,设点A、B的坐标(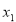 ,
,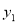 )、(
)、(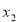 ,
,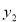 ),利用方程组
),利用方程组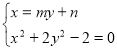 及韦达定理,结合平面向量的数量积,把求△AOB面积S表示成
及韦达定理,结合平面向量的数量积,把求△AOB面积S表示成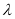 的函数,最后利用基本不等式或一元二次函数的知识求得
的函数,最后利用基本不等式或一元二次函数的知识求得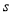 的最大值.
的最大值.
试题解析:【解析】
(1)连接QF,∵|QE|+|QF|=|QE|+|QP|=|PE|=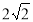 (
(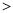 |EF|=2),∴点的轨迹是以E(-1,0) 、F(1,0)为焦点,长轴长
|EF|=2),∴点的轨迹是以E(-1,0) 、F(1,0)为焦点,长轴长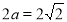 的椭圆,即动点Q的轨迹Γ的方程为
的椭圆,即动点Q的轨迹Γ的方程为 ;
;
(2)依题结合图形知的斜率不可能为零,所以设直线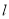 的方程为
的方程为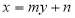 (
( ).∵直线
).∵直线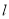 即
即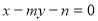 与圆O:
与圆O: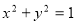 相切,∴有:
相切,∴有:
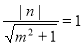 得
得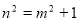 .
.
又∵点A、B的坐标(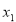 ,
,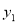 )、(
)、(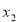 ,
,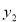 )满足:
)满足: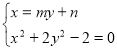
消去整理得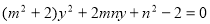 ,
,
由韦达定理得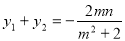 ,
,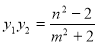 .
.
其判别式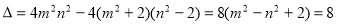 ,
,
又由求根公式有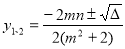 .
.
∵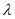 =
=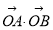 =
=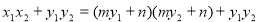
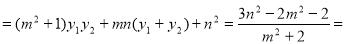
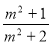 .
.

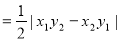
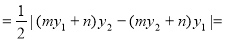
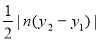
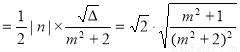
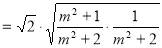 .
.
∵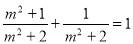 ,且
,且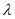
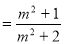 ∈[
∈[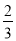 ,
,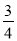 ].
].
∴
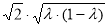 ∈[
∈[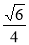 ,
,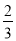 ].
].
考点:1、椭圆的定义与标准方程;2、直线与圆、直线与椭圆的位置关系综合应用.

练习册系列答案
相关题目
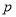 是真命题,
是真命题,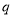 是假命题,则
是假命题,则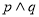 是真命题 B.
是真命题 B.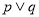 是假命题 C.
是假命题 C.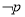 是真命题 D.
是真命题 D.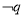 是真命题
是真命题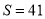 ,则判断框内应填( )
,则判断框内应填( )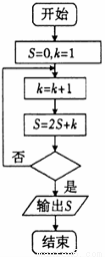
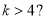 B.
B.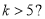 C.
C.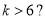 D.
D.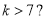
 ,则cos(
,则cos( )的值为 .
)的值为 . ,
,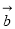 ,两组向量
,两组向量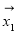 、
、 、
、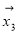 、
、 、
、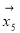 和
和 、
、 、
、 、
、 、
、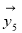 均由2个
均由2个 +
+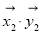 +
+ +
+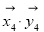 +
+ ,Smin表示S所有可能取值中的最小值.则下列所给5个命题中,所有正确的命题的序号是 .
,Smin表示S所有可能取值中的最小值.则下列所给5个命题中,所有正确的命题的序号是 .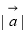 无关;
无关; 无关;④若
无关;④若 ,则Smin>0;
,则Smin>0; ,Smin=
,Smin=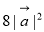 ,则
,则 .
.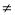 1,函数f(x)=
1,函数f(x)=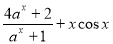 (-1
(-1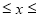 1),设函数f(x)的最大值是M,最小值是N,则 ( )
1),设函数f(x)的最大值是M,最小值是N,则 ( ) 的值是 .
的值是 .
 的展开式中,常数项的值是( ).
的展开式中,常数项的值是( ). B.
B. C.
C. D.180
D.180