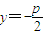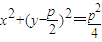题目内容
已知P为抛物线x2=2py(p>0)上的动点,F为抛物线的焦点,过F作抛物线在P点处的切线的垂线,垂足为G,则点G的轨迹方程为
- A.x2+y2=p2
- B.
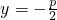
- C.

- D.y=0
D
分析:先设出点G,P的坐标,再由抛物线的方程求出焦点F的坐标并将x表示成y的函数后进行求导,进而得到在P点的切线的斜率,根据在P点的切线的斜率等于由两点表示出直线PG的斜率进而得到一个关系式,根据FG⊥PG得到直线FG的斜率和直线PG的斜率的关系式,最后根据抛物线的关系确定答案.
解答:设G(x,y),P(x0,y0)
由题意可知 F(0, ),y=
),y= ,∴y'=
,∴y'= ,则在P点处的切线的斜率等于
,则在P点处的切线的斜率等于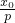
故kPG=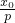 =
= ①
①
∵FG⊥PG∴kFG= ×
×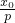 =-1 ②
=-1 ②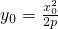 ③
③
联立①②③可消去p,x0,得到y=0
故选D.
点评:本题主要考查抛物线的基本性质和直线和抛物线的综合问题.考查综合运用能力和计算能力.
分析:先设出点G,P的坐标,再由抛物线的方程求出焦点F的坐标并将x表示成y的函数后进行求导,进而得到在P点的切线的斜率,根据在P点的切线的斜率等于由两点表示出直线PG的斜率进而得到一个关系式,根据FG⊥PG得到直线FG的斜率和直线PG的斜率的关系式,最后根据抛物线的关系确定答案.
解答:设G(x,y),P(x0,y0)
由题意可知 F(0,
 ),y=
),y= ,∴y'=
,∴y'= ,则在P点处的切线的斜率等于
,则在P点处的切线的斜率等于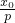
故kPG=
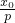 =
= ①
①∵FG⊥PG∴kFG=
 ×
×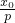 =-1 ②
=-1 ②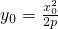 ③
③联立①②③可消去p,x0,得到y=0
故选D.
点评:本题主要考查抛物线的基本性质和直线和抛物线的综合问题.考查综合运用能力和计算能力.

练习册系列答案
相关题目
已知P为抛物线x2=2py(p>0)上的动点,F为抛物线的焦点,过F作抛物线在P点处的切线的垂线,垂足为G,则点G的轨迹方程为( )
| A、x2+y2=p2 | ||||
B、y=-
| ||||
C、x2+(y-
| ||||
| D、y=0 |
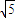 +2
+2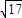 -1
-1