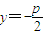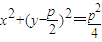题目内容
已知P为抛物线x2=4y上的动点,Q是圆(x-4)2+y2=1上的动点,则点P到点Q的距离与点P到抛物线准线的距离之和的最小值为( )
分析:先根据抛物线方程求得焦点坐标,根据圆的方程求得圆心坐标,根据抛物线的定义可知P到准线的距离等于点P到焦点的距离,进而问题转化为求点P到点Q的距离与点P到抛物线的焦点距离之和的最小值,根据图象可知当P,Q,F三点共线时P到点Q的距离与点P到抛物线的焦点距离之和的最小,为圆心到焦点F的距离减去圆的半径.
解答:解:抛物线x2=4y的焦点为F(0,1),y2+(x-4)2=1的圆心为C(4,0),
根据抛物线的定义可知点P到准线的距离等于点P到焦点的距离,
故问题转化为求P,Q,F三点共线时P到点Q的距离与点P到抛物线的焦点距离之和的最小值,
由于焦点到圆心的距离是
=
点P到点Q的距离与点P到抛物线准线的距离之和的最小值
-1
故选D
根据抛物线的定义可知点P到准线的距离等于点P到焦点的距离,
故问题转化为求P,Q,F三点共线时P到点Q的距离与点P到抛物线的焦点距离之和的最小值,
由于焦点到圆心的距离是
| 1+16 |
| 17 |
点P到点Q的距离与点P到抛物线准线的距离之和的最小值
| 17 |
故选D
点评:本题主要考查了抛物线的应用.考查了学生转化和化归,数形结合等数学思想.

练习册系列答案
相关题目
已知P为抛物线x2=2py(p>0)上的动点,F为抛物线的焦点,过F作抛物线在P点处的切线的垂线,垂足为G,则点G的轨迹方程为( )
| A、x2+y2=p2 | ||||
B、y=-
| ||||
C、x2+(y-
| ||||
| D、y=0 |
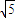 +2
+2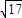 -1
-1