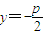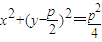题目内容
已知P为抛物线x2=
y上的点，点P到x轴的距离比它到y轴的距离大3，则点P的坐标是
| 1 | 4 |
（1，4）或（-1，4）
（1，4）或（-1，4）
．分析：先设出该点的坐标，点P到x轴的距离比它到y轴的距离大3，得到|x|=y-3，代入抛物线方程求得y值，即可得到所求点的坐标．
解答：解：设抛物线x2=
y上的点P的坐标为（x，y）（y＞0），
由于点P到x轴的距离比它到y轴的距离大3，
则|x|=y-3，
故（y-3）2=
y，解得y=4，
则x=1或-1，
故点P的坐标是（1，4）或（-1，4）
故答案为：（1，4）或（-1，4）．
| 1 |
| 4 |
由于点P到x轴的距离比它到y轴的距离大3，
则|x|=y-3，
故（y-3）2=
| 1 |
| 4 |
则x=1或-1，
故点P的坐标是（1，4）或（-1，4）
故答案为：（1，4）或（-1，4）．
点评：本题主要考查了抛物线的简单性质，属于基础题．
练习册系列答案
优百分课时互动系列答案
相关题目
已知P为抛物线x2=2py（p＞0）上的动点，F为抛物线的焦点，过F作抛物线在P点处的切线的垂线，垂足为G，则点G的轨迹方程为（ ）
| A、x2+y2=p2 | ||||
B、y=-
| ||||
C、x2+(y-
| ||||
| D、y=0 |
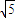+2
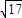-1
