题目内容
5．
如图是一个由圆、三角形、矩形组成的组合图，现用红黄两种颜色为其涂色，每个图形只涂一色，则三个颜色不全相同的概率是（ ）| A． | $\frac{1}{8}$ | B． | $\frac{3}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{4}$ |
分析 首先用分步计数原理分析用两种颜色为3个图形涂色的情况数目，根据题意，分析可得“颜色不全相同”与“颜色全同”为对立事件；易得颜色全同的情况数目，即可得颜色不全相同的情况数目，由古典概型的公式计算可得答案．
解答 解：根据题意，用红黄两种颜色为3个图形涂色，每个图形有2种选择，共2×2×2=8种情况；
其中颜色全部相同的有2种，即全部用红和黄，
则三个形状颜色不全相同的有8-2=6种情况；
故其概率为$\frac{6}{8}$=$\frac{3}{4}$；
故选：D．
点评 本题考查等可能事件的概率，注意题意中对“颜色不全相同”的理解，即与“颜色全同”为对立事件．
练习册系列答案
相关题目
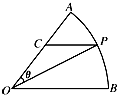在扇形AOB中，圆心角等于$\frac{π}{3}$，半径为4，在弧AB上有一动点P（不与点AB重合），过点P引平行于OB的直线和OA交于点C，设∠AOP=θ，求三角形POC的面积的最大值及此时θ的值．