题目内容
19.在映射f:A→B中,A=B={(x,y)|x,y∈R},且f:(x,y)→(x+y,x-y),则与A中的元素(1,2)对应的B中的元素为(3,-1).分析 根据已知中映射f:A→B的对应法则,f:(x,y)→(x+y,x-y),将A中元素(1,2)代入对应法则,即可得到答案.
解答 解:由映射的对应法则f:(x,y)→(x+y,x-y),
故A中元素(1,2)在B中对应的元素为(1+2,1-2),即(3,-1),
故答案是:(3,-1).
点评 本题考查的知识点是映射的概念,属基础题型,熟练掌握映射的定义,是解答本题的关键.

练习册系列答案
相关题目
14.若复数z满足z=$\frac{10}{6-8i}$,(i为虚数单位),则z的虚部为( )
| A. | 4 | B. | $\frac{4}{5}$ | C. | -4 | D. | -$\frac{4}{5}$ |
11.已知命题p:?x0∈R,使log2x0+x0=2017成立,命题q:?a∈(-∞,0 ),f(x)=|x|-ax(x∈R)为偶函数,则下列命题为真命题的是( )
| A. | p∧q | B. | ?p∧q | C. | p∧?q | D. | ?p∧?q |
8.设等比数列{an}的公比q=2,前n项和为Sn,则$\frac{{S}_{4}}{{a}_{4}}$=( )
| A. | 2 | B. | 4 | C. | $\frac{15}{8}$ | D. | $\frac{17}{8}$ |
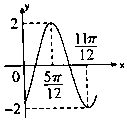 函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则ω=2,φ=-$\frac{π}{3}$.
函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则ω=2,φ=-$\frac{π}{3}$.