Question

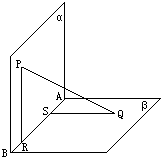
在直二面角α-AB-β中, P∈α, Q∈β, PR⊥AB于R, QS⊥AB于S, PQ与β成45°角, 与α成30°角, 则二面角S-PQ-R的余弦值的平方为_________.

Answer 1

答案：1/3
解析：

解: 连结PS, QR, ∠PQR＝45°, ∠QPS＝30°, T为PQ的中点, 连结RT,  则RT⊥PQ, 过T引TM⊥PQ交PS于M, 连MR, ∠RTM为二面角S-PQ-R的平面角 所以 RM⊥MT, △RMT为直角三角形

提示：

连PS, PQ, 取PQ中点T, 连RT, 过T作TM⊥PQ交PS于M, 连MR, 证明∠RTM为所求 二面角的平面角.