题目内容
设集合A{（x，y）|x+y=6}，集合B={（x，y）|x-y=4}，则A∩B=
{（5，1）}
{（5，1）}
．分析：联立两集合中的方程组成方程组，求出方程组的解即可确定出A与B的交集．
解答：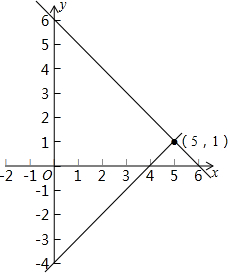
解：由集合A{（x，y）|x+y=6}，集合B{（x，y）|x-y=4}，
联立得：
，
解得：
，
则A∩B={（5，1）}．
故答案为：{（5，1）}
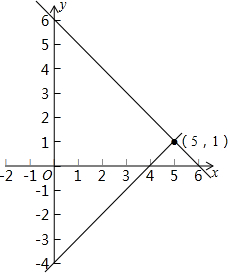解：由集合A{（x，y）|x+y=6}，集合B{（x，y）|x-y=4}，联立得：
|
解得：
|
则A∩B={（5，1）}．
故答案为：{（5，1）}
点评：此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目