题目内容
已知定点F(1,0),动点P在y轴上运动,过点P作PM交x轴于点M,并延长MP到点N,且(1)求动点N的轨迹方程;
(2)直线l与动点N的轨迹交于A、B两点,若![]() ·
·![]() =-4,且4
=-4,且4![]() ≤|
≤|![]() |≤4
|≤4![]() ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
解:(1)设N(x,y),由条件易知P(0,![]() ),M(-x,0).
),M(-x,0).
代入|![]() |=|
|=|![]() |,化简得y2=4x(x>0),
|,化简得y2=4x(x>0),
即为点N的轨迹方程.
(2)设l与y2=4x(x>0)交于A(x1,y1)、B(x2,y2)两点.
当l与x轴垂直时,|AB|=42<46不合题意.
故可设l的方程为y=kx+b(k≠0).
由![]() ·
·![]() =-4,得x1x2+y1y2=-4. ①
=-4,得x1x2+y1y2=-4. ①
由点A、B在抛物线y2=4x(x>0)上,
得 (y1y2)2=16x1x2. ②
(y1y2)2=16x1x2. ②
由①②得y1y2=-8.
又由 ky2-4y+4b=0.
ky2-4y+4b=0.
所以|![]() |2=(1+
|2=(1+![]() )(y2-y1)2
)(y2-y1)2
=(1+![]() )[(y1+y2)2-4y1y2]
)[(y1+y2)2-4y1y2]
=(1+![]() )(
)(![]() +32).
+32).
因为4![]() ≤|
≤|![]() |≤4
|≤4![]() ,
,
所以96≤(1+![]() )(
)(![]() +32)≤480.
+32)≤480.
解得![]() ≤|k|≤1.
≤|k|≤1.
故直线l的斜率k的取值范围是k∈[-1,-![]() ]∪[
]∪[![]() ,1].
,1].

练习册系列答案
相关题目
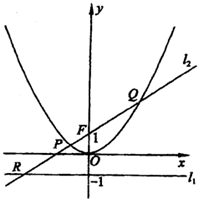 已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.
已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.