题目内容
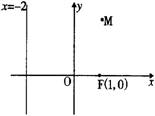
已知定点F(1,0),点P在y轴上运动,点M在x轴上,PM⊥PF,设点M关于点P的对称点为N.(1)求点N轨迹E的方程;
(2)过F作轨迹E的两条互相垂直的弦AB、CD,设AB、CD的中点分别为G、H,求证:直线GH必过定点Q(3,0).
(1)解:设N(x,y),依题意,则x+xm=0,y=2yp.
又PF⊥MN,kPF·kMN=-1,
kPF=-yp,kMN=![]() .
.
代入整理,得y2=4x.
(2)解:设A(xa,ya),B(xb,yb),G(xG,yG),H(xH,yH),直线AB的方程为y=k(x-1),
则 ①②
①②
①-②,得yA+yB=![]() ,即yG=
,即yG=![]() ,代入方程y=k(x-1),解得xG=
,代入方程y=k(x-1),解得xG=![]() +1.
+1.
所以点G坐标为(![]() +1,
+1,![]() ).9分同理可得:点H的坐标为(2k2+1,-2k).
).9分同理可得:点H的坐标为(2k2+1,-2k).
直线GH的斜率为kGH=![]() ,方程为y+2k=
,方程为y+2k=![]() (x-2k2-1),
(x-2k2-1),
整理,得y(1-k2)=k(x-3),不论k为何值,(3,0)均满足方程,所以直线GH恒过定点Q(3,0).

练习册系列答案
相关题目
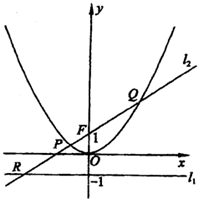 已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.
已知定点F(0,1)和直线l1:y=-1,过定点F与直线l1相切的动圆圆心为点C.