题目内容
若双曲线mx2+ny2=1的一个焦点与抛物线y=
x2的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( )
| 1 |
| 8 |
分析:确定抛物线y=
x2的焦点坐标,双曲线mx2+ny2=1方程化为标准方程,再利用双曲线mx2+ny2=1的一个焦点与抛物线y=
x2的焦点相同,且双曲线的离心率为2,即可求得双曲线的方程.
| 1 |
| 8 |
| 1 |
| 8 |
解答:解:抛物线y=
x2的焦点坐标为(0,2),双曲线mx2+ny2=1方程可化为
-
=1
∴
-
=4
∵双曲线的离心率为2,
∴
=2,∴n=1
∴m=-
∴双曲线的方程为x2-
=1
故选B.
| 1 |
| 8 |
| y2 | ||
|
| x2 | ||
-
|
∴
| 1 |
| n |
| 1 |
| m |
∵双曲线的离心率为2,
∴
| 2 | ||||
|
∴m=-
| 1 |
| 3 |
∴双曲线的方程为x2-
| y2 |
| 3 |
故选B.
点评:本题考查双曲线与抛物线的综合,考查双曲线的标准方程,合理运用性质是关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( )
的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( ) =1
=1 =1
=1
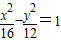
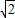 ,且有一个焦点与抛物线y2=2x的焦点重合,则m= .
,且有一个焦点与抛物线y2=2x的焦点重合,则m= . 的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( )
的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( ) =1
=1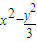 =1
=1