题目内容
若双曲线mx2+ny2=1的一个焦点与抛物线 的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( )
的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( )A.y2+
 =1
=1B.
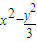 =1
=1C.

D.
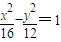
【答案】分析:确定抛物线 的焦点坐标,双曲线mx2+ny2=1方程化为标准方程,再利用双曲线mx2+ny2=1的一个焦点与抛物线
的焦点坐标,双曲线mx2+ny2=1方程化为标准方程,再利用双曲线mx2+ny2=1的一个焦点与抛物线 的焦点相同,且双曲线的离心率为2,即可求得双曲线的方程.
的焦点相同,且双曲线的离心率为2,即可求得双曲线的方程.
解答:解:抛物线 的焦点坐标为(0,2),双曲线mx2+ny2=1方程可化为
的焦点坐标为(0,2),双曲线mx2+ny2=1方程可化为
∴
∵双曲线的离心率为2,
∴ ,∴n=1
,∴n=1
∴m=-
∴双曲线的方程为
故选B.
点评:本题考查双曲线与抛物线的综合,考查双曲线的标准方程,合理运用性质是关键.
 的焦点坐标,双曲线mx2+ny2=1方程化为标准方程,再利用双曲线mx2+ny2=1的一个焦点与抛物线
的焦点坐标,双曲线mx2+ny2=1方程化为标准方程,再利用双曲线mx2+ny2=1的一个焦点与抛物线 的焦点相同,且双曲线的离心率为2,即可求得双曲线的方程.
的焦点相同,且双曲线的离心率为2,即可求得双曲线的方程.解答:解:抛物线
 的焦点坐标为(0,2),双曲线mx2+ny2=1方程可化为
的焦点坐标为(0,2),双曲线mx2+ny2=1方程可化为
∴

∵双曲线的离心率为2,
∴
 ,∴n=1
,∴n=1∴m=-

∴双曲线的方程为

故选B.
点评:本题考查双曲线与抛物线的综合,考查双曲线的标准方程,合理运用性质是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( )
的焦点相同,且双曲线的离心率为2,则该双曲线的方程为( ) =1
=1 =1
=1
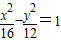
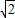 ,且有一个焦点与抛物线y2=2x的焦点重合,则m= .
,且有一个焦点与抛物线y2=2x的焦点重合,则m= .