题目内容
设D是半径为R的圆周上的一定点，在圆周上随机取一点C，连接CD得一弦，若A表示“所得弦的长大于圆内接等边三角形的边长”，则P（A）= ．
考点：几何概型
专题：概率与统计
分析：以点D为一顶点，在圆中作一圆内接正三角形ABD，满足题意点C只能落在劣弧AB上，又圆内接正三角形ABD恰好将圆周3等分，由几何概型计算公式可得．
解答：
解：∴A表示“所得弦的长大于圆内接等边三角形的边长”，
以点D为一顶点，在圆中作一圆内接正三角形ABD，如图所示，
则要满足题意点C只能落在劣弧AB上，又圆内接正三角形ABD恰好将圆周3等分，
故P（A）=
=
，
故答案为：
以点D为一顶点，在圆中作一圆内接正三角形ABD，如图所示，
则要满足题意点C只能落在劣弧AB上，又圆内接正三角形ABD恰好将圆周3等分，
故P（A）=
| 劣弧AB |
| 圆周长 |
| 1 |
| 3 |
故答案为：
| 1 |
| 3 |
点评：本题考查几何概型，其中根据已知条件作图是解决问题的关键，属基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知x为实数，条件p：x2＜x，条件q：
＞2，则p是q的（ ）
| 1 |
| x |
| A、充要条件 |
| B、必要不充分条 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
若全集U=Z，集合A={n|
∈z}，集合B={n|
∈z}，则A∩{CuB}是（ ）
| n |
| 2 |
| n |
| 3 |
| A、{n|n=3k+1，k∈z} |
| B、{n|n=4k或n=4k+2，k∈z} |
| C、{n|n=6k±1，k∈z} |
| D、{n|n=6k±2，k∈z} |
设△ABC的三个内角A，B，C所对的边分别为a，b，c，若△ABC的面积S=c2-（a-b）2，则sinC的值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图是函数f（x）=Asin（ωx+φ）（A＞0，0＜ω＜3，0＜φ＜π）的图象的一部分，则ωφ=（ ）
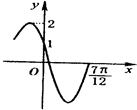
A、
| ||
B、
| ||
C、
| ||
D、
|