题目内容
数列 满足
满足 ,
,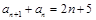 .
.
(Ⅰ)求 、
、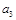 、
、 ;
;
(Ⅱ)求 的表达式;
的表达式;
(Ⅲ)令 ,求
,求 .
.
 满足
满足 ,
,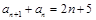 .
.(Ⅰ)求
 、
、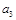 、
、 ;
;(Ⅱ)求
 的表达式;
的表达式;(Ⅲ)令
 ,求
,求 .
.(Ⅰ) 、
、 、
、 ;
;
(Ⅱ)
(Ⅲ)

 、
、 、
、 ;
;(Ⅱ)

(Ⅲ)


试题分析:(Ⅰ)由递推公式即可求出
 、
、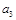 、
、 ;(Ⅱ)方法一:猜想出通项公式,然后用数学归纳法证明;方法二:由递推公式可以构造等比数列,借助等比数列可以求出通项公式;方法二:由递推公式可以构造等差数列,借助等差数列可以求出通项公式;.
;(Ⅱ)方法一:猜想出通项公式,然后用数学归纳法证明;方法二:由递推公式可以构造等比数列,借助等比数列可以求出通项公式;方法二:由递推公式可以构造等差数列,借助等差数列可以求出通项公式;. (Ⅰ)由递推公式:
 、
、 、
、 ; 3分
; 3分(Ⅱ)方法一:猜想:
 ,下面用数学归纳法证明:
,下面用数学归纳法证明: ①
 ,猜想成立;
,猜想成立;② 假设
 时,
时, ,
,则
 ,即
,即 时猜想成立,
时猜想成立,综合①②,由数学归纳法原理知:
 . 8分
. 8分方法二:由
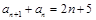 得
得 ,
,所以:
 . 8分
. 8分方法三:由
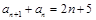 得:
得: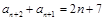 ,两式作差得:
,两式作差得: ,
,于是
 是首项
是首项 ,公差为
,公差为 的等差数列,那么
的等差数列,那么 ,
,且
 是首项
是首项 ,公差为
,公差为 的等差数列,那么
的等差数列,那么 ,
,综上可知:
 . 8分
. 8分(Ⅲ)


 10分
10分
 . 12分.
. 12分.
练习册系列答案
相关题目
 =2
=2 ,
, =3
=3 ,
,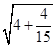 =4
=4 ,…,若
,…,若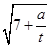 =7
=7 ,(a,t均为正实数),则类比以上等式,可推测a、t的值,a+t= .
,(a,t均为正实数),则类比以上等式,可推测a、t的值,a+t= .  依此类推,第
依此类推,第 个等式为 .
个等式为 . ,由不等式
,由不等式 ,
, ,
, ,….在
,….在
 的
的 次方幂有如下分解方式:
次方幂有如下分解方式:







 的分解中最小的数是73,则
的分解中最小的数是73,则
 ,则依次类推可得
,则依次类推可得 ;
;