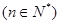题目内容
设函数
(1)若关于x的不等式 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设 ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
(3)证明不等式:

【答案】
(1) (2)p的最小值为0
(3)见解析
(2)p的最小值为0
(3)见解析
【解析】本试题主要考查了导数在研究函数中的运用,求解最值和极值,判定单调性的综合运用,
解:(1)依题意得 然后利用导数分析其最大值即可从而
然后利用导数分析其最大值即可从而
实数m的取值范围为
(2)构造函数

显然,函数 在
在 上为减函数,在
上为减函数,在 上为增函数
上为增函数
则函数 的最小值为
的最小值为
所以,要使方程 至少有一个解,则
至少有一个解,则 ,即p的最小值为0
,即p的最小值为0
(3)由(2)可知:  在
在 上恒成立
上恒成立
所以  ,当且仅当x=0时等号成立
,当且仅当x=0时等号成立
令 ,则
,则 代入上面不等式得:
代入上面不等式得:
即 , 放缩法思想得到结论。
, 放缩法思想得到结论。

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目

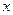 的方程
的方程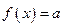 有三个不同的实根,求实数
有三个不同的实根,求实数 的取值范围。
的取值范围。 时,
时, 恒成立。求实数
恒成立。求实数 的取值范围。
的取值范围。
 在
在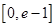 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程 至少有一个解,求
至少有一个解,求 的最小值.
的最小值.

 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.


 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.