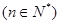题目内容
设函数
(1)若关于x的不等式 在
在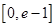 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设 ,若关于x的方程
,若关于x的方程 至少有一个解,求
至少有一个解,求 的最小值.
的最小值.
(3)证明不等式:
【答案】
(1) ;(2)p的最小值为0;(3)见解析。
;(2)p的最小值为0;(3)见解析。
【解析】本试题主要是考查了运用导数来求解函数的方程的解,以及不等式的证明。
(1)因为关于x的不等式 在
在 有实数解,那么只要
有实数解,那么只要 即可,转化为求解函数的
最大值问题。
即可,转化为求解函数的
最大值问题。
(2)设 ,若关于x的方程
,若关于x的方程 至少有一个解,可知分离参数的思想,求解常函数与已知函数有交点时的情况即可。
至少有一个解,可知分离参数的思想,求解常函数与已知函数有交点时的情况即可。
(3)在上一问的基础上,利用单调性得到不等式,ln(1+x) x,来证明不等式。
x,来证明不等式。
(1)依题意得

 ,而函数
,而函数 的定义域为
的定义域为
∴ 在
在 上为减函数,在
上为减函数,在 上为增函数,
上为增函数,
则 在
在 上为增函数
上为增函数

即实数m的取值范围为
(2)

则
显然,函数 在
在 上为减函数,在
上为减函数,在 上为增函数
上为增函数
则函数 的最小值为
的最小值为
所以,要使方程 至少有一个解,则
至少有一个解,则 ,即p的最小值为0
,即p的最小值为0
(3)由(2)可知:  在
在 上恒成立
上恒成立
所以  ,当且仅当x=0时等号成立
,当且仅当x=0时等号成立
令 ,则
,则 代入上面不等式得:
代入上面不等式得:
即 , 即
, 即 
所以, ,
, ,
, ,…,
,…,
将以上n个等式相加即可得到:


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.


 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.

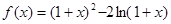
 在
在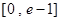 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;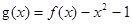 ,若关于x的方程
,若关于x的方程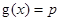 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
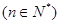
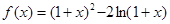
 在
在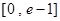 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程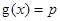 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
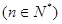

 在
在 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.