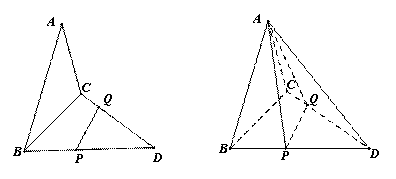
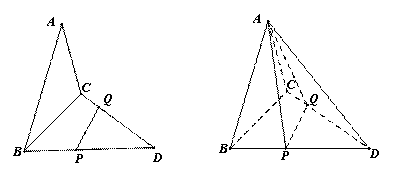
题目内容
如图,已知三角形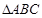 与
与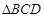 所在平面互相垂直,且
所在平面互相垂直,且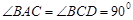 ,
,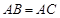 ,
,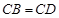 ,点
,点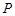 ,
,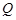 分别在线段
分别在线段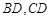 上,沿直线
上,沿直线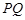 将
将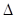
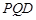 向上翻折,使
向上翻折,使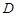 与
与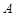 重合.
重合.
(Ⅰ)求证: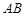
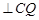 ;
;
(Ⅱ)求直线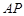 与平面
与平面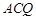 所成的角的正弦值.
所成的角的正弦值.
【答案】
(Ⅰ)证明详见解析;(Ⅱ)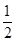 .
.
【解析】
试题分析:(Ⅰ)要证明线线垂直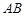
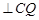 ,由
,由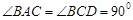 ,有
,有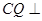 面
面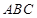 ,从而得到线线垂直
,从而得到线线垂直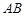
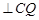 ;(Ⅱ)作
;(Ⅱ)作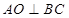 ,垂足为
,垂足为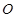 ,则
,则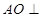 面
面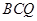 ,连接
,连接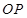 ,得到直线
,得到直线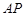 与平面
与平面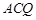 所成的角为
所成的角为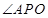 ,求得
,求得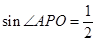 .
.
试题解析:
(Ⅰ)证明 面
面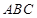
 面
面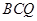 又
又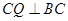
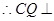 面
面
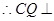
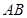
(Ⅱ)解:作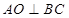 ,垂足为
,垂足为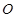 ,则
,则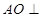 面
面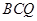 ,
,
连接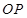
设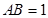 ,则
,则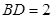 ,设
,设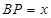
由题意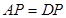
则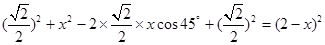
解得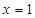
由(Ⅰ)知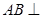 面
面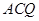
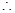 直线
直线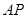 与平面
与平面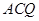 所成的角的正弦值,
所成的角的正弦值,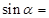
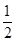 .
.
考点:线与线所成角;线面垂直.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
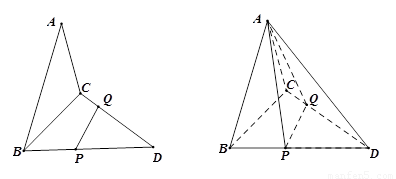
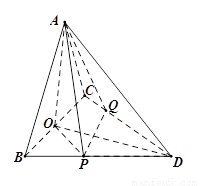
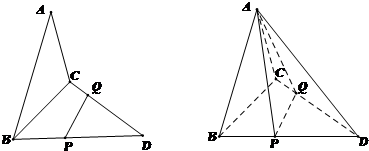 如图,已知三角形△ABC与△BCD所在平面互相垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.
如图,已知三角形△ABC与△BCD所在平面互相垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.