题目内容
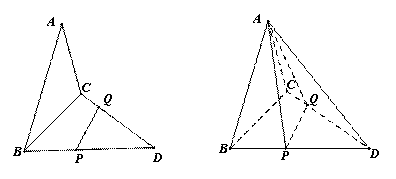
（本题满分14分）如图，已知三角形
与
所在平面互相垂直，且
，
，
，点
,
分别在线段
上，沿直线
将
向上翻折，使
与
重合．
（Ⅰ）求证：
；
（Ⅱ）求直线
与平面
所成的角.
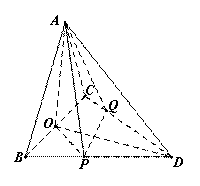
（本小题满分１4分）
（I）证明
面
面
又
面
……………5分
（Ⅱ）解1：作
，垂足为
，则
面，
连接
设
，则
，设
由题意
则
解得
……………9分
由（Ⅰ）知
面
直线
与平面所成的角的正弦值
就是直线与直线所成角的余弦值
， ……………12分
即
=
，
，
即直线与平面所成的角为
……………14分
解2：取
的中点，
的中点
，如图以
所在直线为
轴，以
所在直线为
轴，以
所在直线为
轴，建立空间直角坐标系. ……………6分
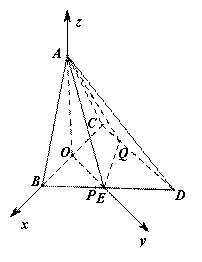不妨设
，则
，……………8分
由
即
，
解得
，所以
， ……………10分
故
设
为平面
的一个法向量，
因为
由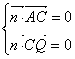
即
所以
……………12分
设直线与平面所成的角为
则
所以
即直线与平面所成的角为 ……………14分
练习册系列答案
相关题目
，E是棱CC1上动点，F是AB中点，
；
、
的边长都是1，平面
平面
在
上移动，点
在
上移动，若
（
）
的长；
为何值时，
与面
所成锐二面角余弦值的大小.
，又E、F分别是C1A和C1B的中点。
（1）求证：EF//平面ABC；
平面C1CBB1；