题目内容
如图所示,直三棱柱ABC-A1B1C1,在底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
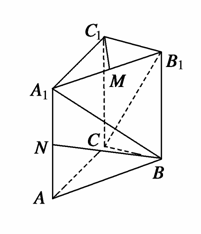
(1)求BN的长;
(2)求异面直线BA1与CB1所成角的余弦值;
(3)求证:A1B⊥C1M.
[解析]
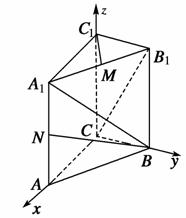
如图所示,以C为原点建立空间直角坐标系C—xyz.
(1)依题意得B(0,1,0),N(1,0,1).
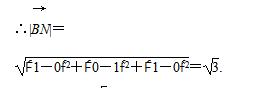 ∴BN的长为
∴BN的长为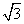 .
.
(2)依题意得A1(1,0,2),B(0,1,0),C(0,0,0),B1(0,1,2),
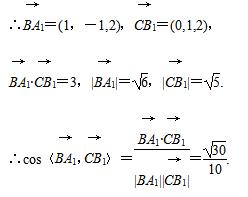 ∴异面直线BA1与CB1所成角的余弦值为
∴异面直线BA1与CB1所成角的余弦值为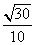 .
.
(3)依题意得C1(0,0,2),M( ,
, ,2),
,2),
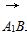 =(-1,1,-2),
=(-1,1,-2),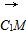 =(
=(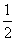 ,
,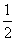 ,0).
,0).
∴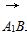 ·
·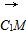 =-
=-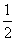 +
+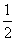 +0=0.
+0=0.
∴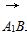 ⊥
⊥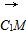 ∴A1B⊥C1M.
∴A1B⊥C1M.

练习册系列答案
相关题目
 ,1,-2) B.(
,1,-2) B.( B.
B.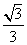
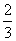 D.
D.

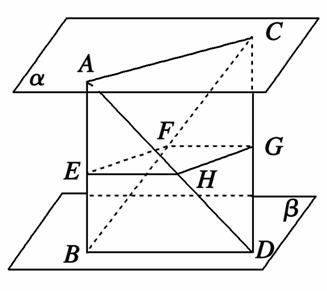
 ,AF=1.M在EF上,且AM∥平面BDE.则M点的坐标为( )
,AF=1.M在EF上,且AM∥平面BDE.则M点的坐标为( )


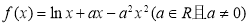 .
.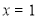 是函数
是函数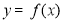 的极值点,求
的极值点,求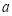 的值;
的值;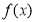 的单调区间.
的单调区间.