题目内容
函数
在[3，4]上单调递增，则实数a的取值范围是
- A.
- B.
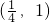
- C.（1，3）
- D.（1，4）
D
分析：先根据函数的定义域，确定a＜4，再利用内外函数的单调性，即可求得实数a的取值范围．
解答：由题意，（x-1）2-a＞0在[3，4]上恒成立，∴a＜4
又t=（x-1）2-a在[3，4]上单调递增，函数在[3，4]上单调递增，
∴a＞1
∴1＜a＜4
故选D．
点评：本题考查复合函数的单调性，考查学生的计算能力，确定内外函数的单调性是关键．
分析：先根据函数的定义域，确定a＜4，再利用内外函数的单调性，即可求得实数a的取值范围．
解答：由题意，（x-1）2-a＞0在[3，4]上恒成立，∴a＜4
又t=（x-1）2-a在[3，4]上单调递增，函数
在[3，4]上单调递增，∴a＞1
∴1＜a＜4
故选D．
点评：本题考查复合函数的单调性，考查学生的计算能力，确定内外函数的单调性是关键．
练习册系列答案
全优点练单元计划系列答案
相关题目
已知点A（x1，y1）在圆（x-2）2+y2=4上运动，点A不与（0，0）重合，点B（4，y0）在直线x=4上运动，动点M（x，y）满足