题目内容
20．已知函数f（x）=|log2x|，若实数a，b（a＜b）满足f（a）=f（b），则a+2017b的范围是（2018，+∞）．分析 画出函数f（x）=|log2x|的图象，可得a＜1＜b，且log2b=-log2a，结合对数的运算性质和对勾函数的图象和性质，可得答案．
解答 解：函数f（x）=|log2x|的图象如下图所示：
若0＜a＜b，且f（a）=f（b），
则a＜1＜b，且log2b=-log2a，
即ab=1，
∴2017b+a=2017b+$\frac{1}{b}$＞2018，（b＞1）
故2a+b的取值范围是（2018，+∞），
故答案为：（2018，+∞）
点评 本题考查的知识点是函数的图象，对数的运算性质，对勾函数的图象和性质，难度中档．
练习册系列答案
相关题目
10．已知命题p：负数的立方都是负数，命题q：正数的对数都是负数，则下列命题中是真命题的是（ ）
| A． | （￢p）∨q | B． | p∧q | C． | （￢p）∨（￢q） | D． | （￢p）∧（￢q） |
11．已知f（x）=$\frac{1}{2}$x+sinx，x∈[-$\frac{π}{2}$，$\frac{π}{2}$]，则导函数f′（x）是（ ）
| A． | 仅有极小值的奇函数 | B． | 仅有极小值的偶函数 | ||
| C． | 仅有极大值的偶函数 | D． | 既有极小值也有极大值的奇函数 |
8．执行如图所示的程序框图，则输出的结果为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
15．设实数x，y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{y≥1}\\{x+y-4≤0}\end{array}\right.$，若对于任意b∈[0，1]，不等式ax-by＞b恒成立，则实数a的取值范围是（ ）
| A． | （$\frac{2}{3}$，4） | B． | （$\frac{2}{3}$，+∞） | C． | （2，+∞） | D． | （4，+∞） |
12．
一个凸多面体，其三视图如图，则该几何体的体积为（ ）
一个凸多面体，其三视图如图，则该几何体的体积为（ ）| A． | 5$\sqrt{2}$ | B． | 6$\sqrt{2}$ | C． | 9 | D． | 10 |
如图所示，游乐场中摩天轮匀速逆时针旋转，每转一圈需要6min，其中心距离地面40.5m，摩天轮的半径为40m，已知摩天轮上点P的起始位置在最低点处，在时刻t（min）时点P距离地面的高度为f（t）=Asin（wt+φ）+h（A＞0，w＞0，-π＜φ＜0，t≥0）．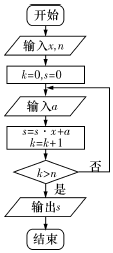
中国古代有计算多项式值的秦九韶算法，如图是实现该算法的程序框图，执行该程序框图，若输入的x=3，n=2，依次输入的a为2，2，5，则输出的s=（ ）