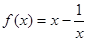题目内容
用定义证明:f(x)=
在(-1,1)上单调递减.
| 2x | x2-1 |
分析:用单调性的定义证明步骤:(1)取值,(2)作差,(3)化简,(4)判号,(5)得结论.
解答:解:在(-1,1)上任取两实数x1,x2,且x1<x2,
则f(x1)-f(x2)=
-
=
,
因为-1<x1<x2<1,所以-1<x1•x2<1,x1•x2+1>0,
x2-x1>0,x1+1>0,x1-1<0,x2+1>0,x2-1<0,
所以f(x1)-f(x2)>0,即f(x1)>f(x2),
所以f(x)=
在(-1,1)上单调递减.
则f(x1)-f(x2)=
| 2x1 |
| x12-1 |
| 2x2 |
| x22-1 |
| 2(x1x2+1)(x2-x1) |
| (x1+1)(x1-1)(x2+1)(x2-1) |
因为-1<x1<x2<1,所以-1<x1•x2<1,x1•x2+1>0,
x2-x1>0,x1+1>0,x1-1<0,x2+1>0,x2-1<0,
所以f(x1)-f(x2)>0,即f(x1)>f(x2),
所以f(x)=
| 2x |
| x2-1 |
点评:本题考察函数单调性的证明,主体部分是化简和判号,要细心.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目