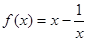Question

用定义证明函数f(x)=

ax+1

x+2

(a≠2)在（-2，+∞）上的单调性．

Answer 1

分析：用定义证明函数f（x）在（-2，+∞）上的单调性，其基本步骤是一取值，二作差，三判正负，四下结论；这里须对a讨论．

解答：证明；∵函数f（x）=

ax+1

x+2

=

a(x+2)-2a+1

x+2

=a+

1-2a

x+2

，
∴任取x₁，x₂∈（-2，+∞），且x₁＜x₂，
则f（x₁）-f（x₂）=（a+

1-2a

x1+2

）-（a+

1-2a

x2+2

）=

1-2a

x1+2

-

1-2a

x2+2

=

(1-2a)(x2-x1)

(x1+2)(x2+2)

；
∵-2＜x₁＜x₂，∴x₂-x₁＞0，（x₁+2）（x₂+2）＞0，
∴当1-2a＞0，即a＜

1

2

时，f（x₁）-f（x₂）＞0，即f（x₁）＞f（x₂），是减函数；
当1-2a＜0，即a＞

1

2

（且a≠2）时，f（x₁）-f（x₂）＜0，即f（x₁）＜f（x₂），是增函数；
所以，在（-2，+∞）上，当a＜

1

2

时，f（x）是减函数，a＞

1

2

且a≠2时，f（x）是增函数．

点评：本题考查了用定义证明函数的单调性问题，是基础题．