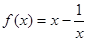Question

用定义证明函数f(x)=x+

2+x

在其定义域上的单调性，并求函数在[2，7]上的最值．

Answer 1

分析：根据函数单调性的定义，首先在所给区间上任设两个数并规定大小，然后通过作差法分析获得两数对应函数值之间的大小关系即可；利用单调性，可求函数在[2，7]上的最值．

解答：证明：函数f(x)=x+

2+x

的定义域为[-2，+∞），…（2分）
设任意x₁，x₂∈[-2，+∞），且x₁＜x₂，则x₁-x₂＜0，…（3分）
所以f（x₁）-f（x₂）=x1+

2+x1

-x2-

2+x2

=(x1-x2)+

2+x1

-

2+x2

=(x1-x2)+

x1-x2

2+x1 + 2+x2

＜0…（7分）
所以函数f(x)=x+

2+x

在其定义域上是增函数．…（8分）
所以函数在[2，7]上的最大值为f(7)=7+

2+7

=10，…（10分）
函数在[2，7]上的最小值为f(2)=2+

2+2

=4．…（12分）

点评：本题考查的是函数单调性的判断和应用问题，解答的关键是作差法并化简．