题目内容
曲线y=x2+bx+c在点P（x0，f（x0））处切线的倾斜角的取值范围为
，则点P到该曲线对称轴距离的取值范围为
- A.[0，1]
- B.
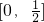
- C.
- D.
B
分析：先由导数的几何意义，得到x0的范围，再求出其到对称轴的范围．
解答：∵过P（x0，f（x0））的切线的倾斜角的取值范围是，
∴f′（x0）=2x0+b∈[0，1]，x0∈[-
]
∴P到曲线y=f（x）对称轴x=-
b的距离d=x0-（-b ）=x0+b，
∵x0∈[-]
∴d=x0+b∈．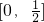
故选B．
点评：本题中是对导数的几何意义的考查，计算时，对范围的换算要细心．考查计算能力．
分析：先由导数的几何意义，得到x0的范围，再求出其到对称轴的范围．
解答：∵过P（x0，f（x0））的切线的倾斜角的取值范围是
，∴f′（x0）=2x0+b∈[0，1]，x0∈[-
]∴P到曲线y=f（x）对称轴x=-
b的距离d=x0-（-b ）=x0+b，∵x0∈[-
]∴d=x0+
b∈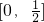．故选B．
点评：本题中是对导数的几何意义的考查，计算时，对范围的换算要细心．考查计算能力．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
，则点P到该曲线对称轴距离的取值范围为（ ）
，则点P到该曲线对称轴距离的取值范围为（ ）
，则点P到该曲线对称轴距离的取值范围为（ ）
，则点P到该曲线对称轴距离的取值范围为（ ）
