题目内容

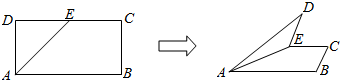
7．如图，在矩形ABCD中，AB=8，BC=4，E为DC边的中点，沿AE将△ADE折起，在折起过程中，有几个正确（　　）
①ED⊥平面ACD   ②CD⊥平面BED    ③BD⊥平面ACD   ④AD⊥平面BED．
A．1个B．2个C．3个D．4个

分析 利用线面垂直的判定定理求解．

解答 解：∵在矩形ABCD中，AB=8，BC=4，E为DC边的中点，
∴在折起过程中，D点在平面BCE上的投影如右图．
∵DE与AC所成角不能为直角，
∴DE不会垂直于平面ACD，故①错误；
只有D点投影位于Q2位置时，即平面AED与平面AEB重合时，
才有BE⊥CD，此时CD不垂直于平面AEBC，
故CD与平面BED不垂直，故②错误；
BD与AC所成角不能成直线，
∴BD不能垂直于平面ACD，故③错误；
∵AD⊥ED，并且在折起过程中，有AD⊥BC，
∴存在一个位置使AD⊥BE，
∴在折起过程中AD⊥平面BED，故④正确．
故选：A．

点评 本题考查命题真假的判断，是中档题，解题时要认真审题，注意线面垂直的判定定理的合理运用．

练习册系列答案
相关题目
17．若f（x）=5sinx，则$f'（\frac{π}{2}）$=0．
18．已知函数f（x）=loga（x-3）+5（a＞0且a≠1）的图象过定点P，角α的始边与x轴正半轴重合且终边过点P，则$\frac{cos（\frac{11π}{2}-α）sin（\frac{9π}{2}+α）}{cos（\frac{π}{2}+α）sin（-π-α）}$的值为（　　）
A．$\frac{3}{5}$B．$\frac{2}{5}$C．$\frac{4}{5}$D．$\frac{5}{4}$
15．已知函数$f（x）=\left\{\begin{array}{l}{log_2}（{1-x}）+1，-1≤x＜k\\{x^2}-2x+1，k≤x≤a\end{array}\right.$，若存在实数k使函数f（x）的值域为[0，2]，则实数a的取值范围为[$\frac{1}{2}$，1+$\sqrt{2}$]．
2．圆C过点A（6，4），B（1，-1），且圆心在直线l：x-5y+7=0上．
（1）求圆C的方程；
（2）P为圆C上的任意一点，定点Q（7，0），求线段PQ中点M的轨迹方程．
12．幂函数y=f（x）的图象经过点A（2，4），则曲线y=f（x）在点A处切线的斜率为（　　）
A．4B．-4C．2D．-2
19．函数y=ax-cosx为R上的减函数的a的范围为a＜-1．
16．f′（x）是f（x）的导函数，若f′（x）的图象如图所示，则f（x）的图象可能是（　　）
A．B．C．D．
17．下列语句中，不是命题的语句是（　　）
A．12＞5B．若a为正无理数，则$\sqrt{a}$也是正无理数
C．正弦函数是周期函数吗？D．π∈{1，2，3，4}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网