题目内容

已知等比数列{an}的各项都是正数，且a3-a2=10，a1+a2+a3=35，则数列{an}的前6项和为
 
．
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：根据条件求出数列的公比与首项，即可得到结论．
解答： 解：设公比为q（q＞0），则
∵a3-a2=10，a1+a2+a3=35，
∴a1q2-a1q=10，a1+a1q+a1q2=35，
两式相除可得5q2-9q-2=0，
∵q＞0，∴q=2，
∴a1=5，
∴数列{an}的前6项和为
5(1-26)
1-2
=155．
故答案为：155．
点评：本题主要考查等比数列的前n项和的计算，根据条件求出公比是解决本题的关键．
练习册系列答案
相关题目
已知sinα=-
4
5
，且α是第三象限角，
（Ⅰ）求cos（α-
π
6
）的值
（Ⅱ）求tan（α+
π
4
）的值．
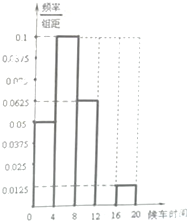常州公交公司为了调整302线路发车的时间间隔，在某站点对乘客进行了候车时间的调查，以下是候车时间的频率分布表和频率分布直方图．
候车时间（分钟） 频数 频率
[0，4） 4 0.2
[4，8） 8 0.4
[8，12） y
[12，16） z
[16，20] 0.05
合计 x 1
（1）求实数x，y，z的值；
（2）补全频率分布直方图；
（3）估计乘客在该站点的平均候车时间．
设复数z满足z（3+4i）=7+i（i为虚数单位），则|z|=
 
．
如图，为了估计阴影部分的面积，向边长为6的正方形内随机投掷800个点，恰有200个点落在阴影部分内，据此，可估计阴影部分的面积为
 
．
已知集合A={x|x2-2x-15＞0}，则∁RA=
 
．
关于函数f（x）=4sin（2x-
π
3
）（x∈R），有下列命题：
（1）y=f（x+
4π
3
）为偶函数；
（2）要得到函数g（x）=-4sin2x的图象，只需将f（x）的图象向右平移
π
3
个单位；
（3）y=f（x）的图象关于直线x=-
π
12
对称．
其中正确命题的序号为：
 
．
根据给出的算法框图，计算f（-2）+f（1）=
 
．
已知2x+y=2，且x，y都为正实数，则xy+
1
xy
的最小值为（　　）
A、2
B、
3
2
2
C、
9
8
D、
5
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网