题目内容
4．数列{an}为等比数列，若a3=-3，a4=6，则a6=（ ）| A． | -24 | B． | 12 | C． | 18 | D． | 24 |
分析 利用等比数列的通项公式及其性质即可得出．
解答 解：设等比数列{an}的公比为q，∵a3=-3，a4=6，
∴q=$\frac{{a}_{4}}{{a}_{3}}$=-2，
则a6=${a}_{4}×{q}^{2}$=6×（-2）2=24．
故选：D．
点评 本题考查了等比数列的通项公式及其性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
中考利剑中考试卷汇编系列答案
相关题目
12．样本的数据如下：3，4，4，x，5，6，6，7，若该样本平均数为5，则样本方差为（ ）
| A． | 1.2 | B． | 1.3 | C． | 1.4 | D． | 1.5 |
9．
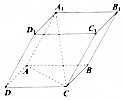如图，在平行六面体A1C中，AD=AB=AA1=4，∠A1AB=60°，∠BAD=90°，∠A1AD=120°，cos∠A1AC=（ ）
如图，在平行六面体A1C中，AD=AB=AA1=4，∠A1AB=60°，∠BAD=90°，∠A1AD=120°，cos∠A1AC=（ ）| A． | -$\frac{\sqrt{3}}{2}$ | B． | -$\frac{1}{2}$ | C． | 0 | D． | $\frac{1}{2}$ |
12．已知函数f（x）=sin（ωx+$\frac{π}{3}$）-$\frac{1}{2}$cos（ωx-$\frac{7π}{6}$）（ω＞0）的最小正周期为2π，则f（-$\frac{π}{6}$）=（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{3}{2}$ | C． | $\frac{3\sqrt{3}}{4}$ | D． | $\frac{3\sqrt{3}}{2}$ |
13．设命题p：?x∈R，x2+1＞0，则￢p为（ ）
| A． | $?{x_0}∈R，{x^2}+1＞0$ | B． | $?{x_0}∈R，{x^2}+1≤0$ | C． | $?{x_0}∈R，{x^2}+1＜0$ | D． | $?{x_0}∈R，{x^2}+1≤0$ |