题目内容
若| |=
|= ,|
,| |=2且(
|=2且( -
- )⊥
)⊥ ,则
,则 与
与 的夹角是
的夹角是
- A.

- B.

- C.

- D.

B
分析:利用向量垂直的充要条件列出方程,利用向量的运算律化简等式,利用向量的数量积公式求出向量夹角的余弦值,求出向量的夹角.
解答:设向量的夹角为θ,
∵ ,
,
∴ ,
,
∴ ,
,
即2-2 cosθ=0,
cosθ=0,
∴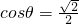 ,
,
∵0≤θ≤π,
∴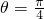 ,
,
故选B.
点评:本题考查向量垂直的充要条件、向量的运算律、向量的数量积公式.
分析:利用向量垂直的充要条件列出方程,利用向量的运算律化简等式,利用向量的数量积公式求出向量夹角的余弦值,求出向量的夹角.
解答:设向量的夹角为θ,
∵
 ,
,∴
 ,
,∴
 ,
,即2-2
 cosθ=0,
cosθ=0,∴
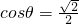 ,
,∵0≤θ≤π,
∴
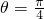 ,
,故选B.
点评:本题考查向量垂直的充要条件、向量的运算律、向量的数量积公式.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目