题目内容
在如图所示的四棱锥A—BCDE中,AD⊥底面BCDE,AC⊥BC,AE⊥BE.(1)求证:A、B、C、D、E五点都在以AB为直径的同一球面上.
(2)若∠CBE=90°,CE=
,AD=1,求B、D两点的球面距离.
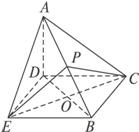
(1)证明:取AB中点P,
由题设条件知△AEB、△ADB、△ABC都是直角三角形,
故PE=PD=PC=AB=PA=PB,所以A、B、C、D、E五点在同一球面上.
(2)解析:由题意知BCDE是矩形,所以BD=CE=
.
在Rt△ADB中,AB=2,AD=1,
所以∠DPB=120°,D、B的球面距离为
.
练习册系列答案
相关题目
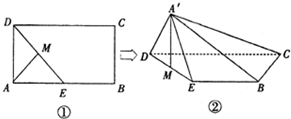如图①，四边形ABCD是矩形，AB=2AD=2a，E为AB的中点，在四边形ABCD中，将△AED沿DE折起，使A到A′位置，且A′M⊥BC，得到如图②所示的四棱锥A′-BCDE．
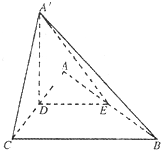（2013•郑州一模）如图，△ABC是等腰直角三角形∠ACB=90°，AC=2a，D，E分别为AC，AB的中点，沿DE将△ADE折起，得到如图所示的四棱锥A′-BCDE
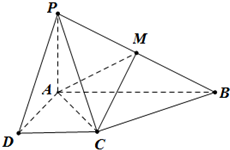在如图所示的四棱锥P-ABCD中，已知 PA⊥平面ABCD，AB∥DC，∠DAB=90°，PA=AD=DC=1，AB=2，M为PB的中点．