题目内容
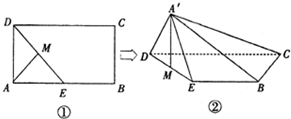 如图①,四边形ABCD是矩形,AB=2AD=2a,E为AB的中点,在四边形ABCD中,将△AED沿DE折起,使A到A′位置,且A′M⊥BC,得到如图②所示的四棱锥A′-BCDE.
如图①,四边形ABCD是矩形,AB=2AD=2a,E为AB的中点,在四边形ABCD中,将△AED沿DE折起,使A到A′位置,且A′M⊥BC,得到如图②所示的四棱锥A′-BCDE.(Ⅰ)求证:A′M⊥平面BCDE;
(Ⅱ)求四棱锥A′-BCDE的体积;
(Ⅲ)判断直线A′D与BC的位置关系.
分析:(I)证明A′M⊥DE,结合A′M⊥BC,利用线面垂直的判定定理,即可得到结论;
(II)由(I)知A′M⊥平面BCDE,则A′M是四棱锥A′-BCDE的高,利用体积公式,即可求四棱锥A′-BCDE的体积;
(Ⅲ)直线A′D与BC是异面直线,利用反证法进行证明即可.
(II)由(I)知A′M⊥平面BCDE,则A′M是四棱锥A′-BCDE的高,利用体积公式,即可求四棱锥A′-BCDE的体积;
(Ⅲ)直线A′D与BC是异面直线,利用反证法进行证明即可.
解答: (I)证明:在△A′DE中,A′E⊥A′D,A′E=A′D,
(I)证明:在△A′DE中,A′E⊥A′D,A′E=A′D,
∵M为DE的中点,
∴A′M⊥DE,
∵A′M⊥BC,又DE与BC相交,
∴A′M⊥平面BCDE.
(II)解:由(I)知A′M⊥平面BCDE,则A′M是四棱锥A′-BCDE的高,
在△A′DE中,A′E⊥A′D,A′E=A′D=a,则A′M=
a.
∵四边形BCDE是直角梯形,BE=BC=a,DC=2a,∴四边形BCDE的面积S=
=
a2
∴四棱锥A′-BCDE的体积V=
S•A′M+
×
a2×
a=
a3
(III)解:直线A′D与BC是异面直线,理由如下:
假设直线A′D与BC共面,则直线A′D与BC确定平面α,所以A′、D、B、C,都在平面α上
∵D,B,C确定平面BCDE,则A′在平面BCDE上,这与已知矛盾
∴直线A′D与BC是异面直线.
 (I)证明:在△A′DE中,A′E⊥A′D,A′E=A′D,
(I)证明:在△A′DE中,A′E⊥A′D,A′E=A′D,∵M为DE的中点,
∴A′M⊥DE,
∵A′M⊥BC,又DE与BC相交,
∴A′M⊥平面BCDE.
(II)解:由(I)知A′M⊥平面BCDE,则A′M是四棱锥A′-BCDE的高,
在△A′DE中,A′E⊥A′D,A′E=A′D=a,则A′M=
| ||
| 2 |
∵四边形BCDE是直角梯形,BE=BC=a,DC=2a,∴四边形BCDE的面积S=
| (a+2a)a |
| 2 |
| 3 |
| 2 |
∴四棱锥A′-BCDE的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| ||
| 4 |
(III)解:直线A′D与BC是异面直线,理由如下:
假设直线A′D与BC共面,则直线A′D与BC确定平面α,所以A′、D、B、C,都在平面α上
∵D,B,C确定平面BCDE,则A′在平面BCDE上,这与已知矛盾
∴直线A′D与BC是异面直线.
点评:本题考查线面垂直,考查四棱锥体积的计算,考查反证法,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠C=135°,沿对角线AC将△ABC折起,使平面ABC与平面ACD互相垂直.
如图,平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠C=135°,沿对角线AC将△ABC折起,使平面ABC与平面ACD互相垂直. (1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知
(1)如图,平行四边形ABCD中,M、N分别为DC、BC的中点,已知 如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,
如图,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2, 在平面直角坐标系xoy中,已知四边形OABC是平行四边形,A(4,0),C(1,
在平面直角坐标系xoy中,已知四边形OABC是平行四边形,A(4,0),C(1,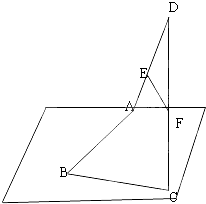 已知:如图,空间四边形ABCD中,E、F分别是DA、DC的中点.求证:EF∥平面ABC.
已知:如图,空间四边形ABCD中,E、F分别是DA、DC的中点.求证:EF∥平面ABC.