题目内容
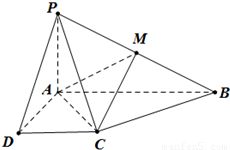
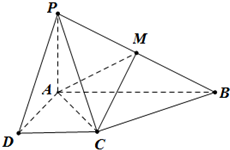 在如图所示的四棱锥P-ABCD中,已知 PA⊥平面ABCD,AB∥DC,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.
在如图所示的四棱锥P-ABCD中,已知 PA⊥平面ABCD,AB∥DC,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.(Ⅰ)求证:MC∥平面PAD;
(Ⅱ)求直线MC与平面PAC所成角的余弦值;
(Ⅲ)求二面角A-PB-C的平面角的正切值.
分析:(Ⅰ)取PA的中点E,连接ME,DE,证明四边形DCME为平行四边形,可得MC∥DE,利用线面平行的判定,可得MC∥平面PAD;
(Ⅱ)取PC中点N,则可得∠MCN为直线MC与平面PAC所成角,从而可求直线MC与平面PAC所成角的余弦值;
(Ⅲ)取AB的中点H,连接CH,过H作HG⊥PB于G,连接CG,则∠CGH为二面角A-PB-C的平面角,由此可求二面角A-PB-C的平面角的正切值.
(Ⅱ)取PC中点N,则可得∠MCN为直线MC与平面PAC所成角,从而可求直线MC与平面PAC所成角的余弦值;
(Ⅲ)取AB的中点H,连接CH,过H作HG⊥PB于G,连接CG,则∠CGH为二面角A-PB-C的平面角,由此可求二面角A-PB-C的平面角的正切值.
解答: (Ⅰ)证明:如图,取PA的中点E,连接ME,DE,∵M为PB的中点,
(Ⅰ)证明:如图,取PA的中点E,连接ME,DE,∵M为PB的中点,
∴EM∥AB,且EM=
AB.
又∵AB∥DC,且DC=
AB,
∴EM∥DC,且EM=DC
∴四边形DCME为平行四边形,∴MC∥DE,
又MC?平面PAD,DE?平面PAD
所以MC∥平面PAD;
(Ⅱ)解:取PC中点N,则MN∥BC
∵PA⊥平面ABCD,∴PA⊥BC,
又AC2+BC2=2+2=AB2,∴AC⊥BC
∵PA∩AC=A,PA⊥BC,AC⊥BC
∴BC⊥平面PAC,
∴MN⊥平面PAC
∴∠MCN为直线MC与平面PAC所成角,
∵NC=
PC=
,MC=
PB=
,
∴cos∠MCN=
=
;
(Ⅲ)解:取AB的中点H,连接CH,则由题意得CH⊥AB
又PA⊥平面ABCD,所以PA⊥CH,则CH⊥平面PAB.
所以CH⊥PB,
过H作HG⊥PB于G,连接CG,则PB⊥平面CGH,所以CG⊥PB,则∠CGH为二面角A-PB-C的平面角.
∵PA=1,∴CH=1,AB=2,
∵PA=1,AB=2,∴PB=
=
∴GH=BHsin∠PBA=BH•
=
,∴tan∠CGH=
=
故二面角A-PB-C的平面角的正切值为
.
 (Ⅰ)证明:如图,取PA的中点E,连接ME,DE,∵M为PB的中点,
(Ⅰ)证明:如图,取PA的中点E,连接ME,DE,∵M为PB的中点,∴EM∥AB,且EM=
| 1 |
| 2 |
又∵AB∥DC,且DC=
| 1 |
| 2 |
∴EM∥DC,且EM=DC
∴四边形DCME为平行四边形,∴MC∥DE,
又MC?平面PAD,DE?平面PAD
所以MC∥平面PAD;
(Ⅱ)解:取PC中点N,则MN∥BC
∵PA⊥平面ABCD,∴PA⊥BC,
又AC2+BC2=2+2=AB2,∴AC⊥BC
∵PA∩AC=A,PA⊥BC,AC⊥BC
∴BC⊥平面PAC,
∴MN⊥平面PAC
∴∠MCN为直线MC与平面PAC所成角,
∵NC=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴cos∠MCN=
| NC |
| MC |
| ||
| 5 |
(Ⅲ)解:取AB的中点H,连接CH,则由题意得CH⊥AB
又PA⊥平面ABCD,所以PA⊥CH,则CH⊥平面PAB.
所以CH⊥PB,
过H作HG⊥PB于G,连接CG,则PB⊥平面CGH,所以CG⊥PB,则∠CGH为二面角A-PB-C的平面角.
∵PA=1,∴CH=1,AB=2,
∵PA=1,AB=2,∴PB=
| PA2+AB2 |
| 5 |
∴GH=BHsin∠PBA=BH•
| PA |
| AB |
| 1 | ||
|
| CH |
| GH |
| 5 |
故二面角A-PB-C的平面角的正切值为
| 5 |
点评:本题考查线面平行,考查线面角,面面角,考查学生的计算能力,掌握线面平行,面面垂直的判定,正确作出线面角是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•河池模拟)在如图所示的四棱锥P-ABCD中,已知 PA⊥平面ABCD,AB∥DC,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.
(2013•河池模拟)在如图所示的四棱锥P-ABCD中,已知 PA⊥平面ABCD,AB∥DC,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.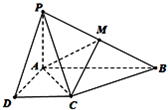 在如图所示的四棱锥P-ABCD中,已知 PA⊥平面ABCD,AB∥DC,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.
在如图所示的四棱锥P-ABCD中,已知 PA⊥平面ABCD,AB∥DC,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.