题目内容
如图直三棱柱ABC﹣A1B1C1的体积为V,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B﹣APQC的体积为( )

|
| A. |
| B. |
| C. |
| D. |
|
考点:
组合几何体的面积、体积问题.
专题:
计算题.
分析:
把问题给理想化,认为三棱柱是正三棱柱,设底面边长a和侧棱长h均为1,P、Q分别为侧棱AA′,CC′上的中点
求出底面面积高,即可求出四棱锥B﹣APQC的体积.
解答:
解:不妨设三棱柱是正三棱柱,设底面边长a和侧棱长h均为1
则V=SABC•h=![]() •1•1•
•1•1•![]() •1=
•1=![]() 认为P、Q分别为侧棱AA′,CC′上的中点
认为P、Q分别为侧棱AA′,CC′上的中点
则V B﹣APQC=![]() SAPQC•
SAPQC•![]() =
=![]() (其中
(其中![]() 表示的是三角形ABC边AC上的高)
表示的是三角形ABC边AC上的高)
所以V B﹣APQC=![]() V
V
故选B
点评:
本题考查几何体的体积,考查计算能力,特殊化法,在解题中有独到效果,本题还可以再特殊点,四棱锥变为三棱锥解答更好.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
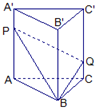 如图直三棱柱ABC-A1B1C1的体积为V,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B-APQC的体积为( )
如图直三棱柱ABC-A1B1C1的体积为V,点P、Q分别在侧棱AA1和CC1上,AP=C1Q,则四棱锥B-APQC的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
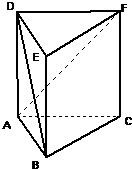 16、如图直三棱柱ABC-DEF中,∠CAB是直角,AB=AC=CF,则异面直线DB与AF所成角的度数为
16、如图直三棱柱ABC-DEF中,∠CAB是直角,AB=AC=CF,则异面直线DB与AF所成角的度数为
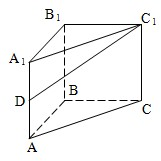 (2008•徐汇区二模)如图直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,∠ABC=90°,AC=2,D是AA1的中点
(2008•徐汇区二模)如图直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,∠ABC=90°,AC=2,D是AA1的中点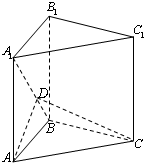 (2012•咸阳三模)如图直三棱柱ABC-A1B1C1中,AC=CC1=2,AB=BC,D是BA1上一点,且AD⊥平面A1BC.
(2012•咸阳三模)如图直三棱柱ABC-A1B1C1中,AC=CC1=2,AB=BC,D是BA1上一点,且AD⊥平面A1BC.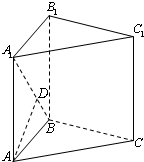 (2012•咸阳三模)如图直三棱柱ABC-A1B1C1中,AC=CC1=2,AB=BC,D是BA1上一点,且AD⊥平面A1BC.
(2012•咸阳三模)如图直三棱柱ABC-A1B1C1中,AC=CC1=2,AB=BC,D是BA1上一点,且AD⊥平面A1BC.