题目内容
已知函数
的图象按向量
平移后得到的图象关于原点对称，且
。
（1）求a，b，c的值；
（2）设
，
。求证：
；
（3）定义函数
。当n为正整数时，求证：
。
的图象按向量平移后得到的图象关于原点对称，且。 （1）求a，b，c的值；
（2）设
，。求证：；（3）定义函数
。当n为正整数时，求证：。 （1）解：
，
因为图象关于原点对称，
∴
即
，
∵a∈N，
∴
，
∴c=0，
∴
又
，
∴
，
由条件知，
。
（2）证明：
，
∴
，
∴
，
但
，
，
∴
由于
，
∴
∴
即
。
（3）证明：由（1）知，
，
令
，
由不等式
，得
，
将这些同向不等式相乘得
故
，
即
。
，因为图象关于原点对称，
∴
即
，∵a∈N，
∴
，∴c=0，
∴
又
，∴
，由条件知，
。（2）证明：
，∴
，∴
，但
，，∴
由于
，∴
∴
即
。（3）证明：由（1）知，
，令
，由不等式
，得，将这些同向不等式相乘得
故
，即
。
练习册系列答案
相关题目
的图象按向量
平移后得到函数y=
的图象，数列
满足
（n≥2，nÎN*）．
，数列
满足
，求证：数列
满足
的前
项和.
; ②数列
中是否存在最大项与最小项，若存在，求出最大项与最小项，若不存在，说明理由.
的图象按向量n=(b,0)平移后得到函数
的图象,则函数
=ax-b (a＞0且a≠1)的反函数
(x)的图象恒过定点
的图象按向量
平移得到函数
的图象．
，求函数
的单调递增区间和最值．
的图象按向量
平移得到函数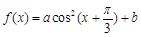
的图象．
，求函数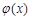
的单调递增区间和最值．