题目内容
(1)求函数y=3ex+xsinx的导数;
(2)已知函数y=lnx+ax2+bx在x=1和x=2处有极值,求实数a,b的值.
(2)已知函数y=lnx+ax2+bx在x=1和x=2处有极值,求实数a,b的值.
解:(1)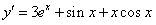 ;
;
(2)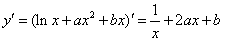 ,
,
∵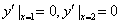 ,
,
∴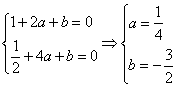 。
。
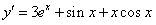 ;
;(2)
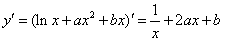 ,
,∵
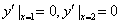 ,
,∴
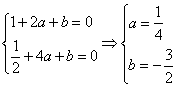 。
。
练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
题目内容
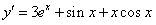 ;
;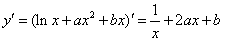 ,
,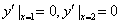 ,
,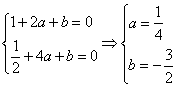 。
。
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案